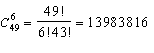
В. Булычев, г. Калуга
Введение элементов теории вероятностей в школьный курс математики, о необходимости которого так долго говорили все наши ученые, наконец-то произошло. Сегодня мы имеем первый учебник [1] для массовой школы (притом для 6-го класса!), содержащий главу о вероятности. В результате многие учителя оказались в нелегком положении. Большинство из них не помнит даже самих <элементов>, не говоря уже о какой-то специальной методике их преподавания в школе. Вероятность всегда входила и входит в обязательную программу любого математического факультета, но стандартный вузовский курс вероятности, как правило, почти не касается проблем интерпретации вероятностных моделей, без чего трудно обойтись в школе (да и в жизни, пожалуй, тоже). Знание аксиоматики Колмогорова и интеграла Лебега здесь не всегда помогает. Хорошая тому иллюстрация - задачи последнего раздела учебника [1] <Вероятность вокруг нас>, некоторые из них мы и собираемся здесь обсудить. Оговоримся сразу, что точное решение большинства из этих задач в 6-м классе невозможно. Но, во-первых, оно далеко не всегда необходимо (даже в математике!), а во-вторых, авторы оставляют возможность вернуться к обсуждению этих задач позже, в старших классах (хочется верить, что эта возможность у них будет). Еще одна особенность всех задач - их проблемность. Это не задачи-упражнения, а задачи-проблемы. Именно поэтому многие из них имеют не совсем <математические> формулировки, оставляя ученику возможность самостоятельно сделать постановку, точно описать условие и сформулировать вопрос. Рассмотрим несколько задач.
1272 Данила на карточке спортлото (6 из 49) отметил номера 1, 2, 3, 4, 5, 6. Наташа на своей карточке отметила номера 5, 12, 17, 23, 35, 49. Как вы думаете, выигрыш какого набора чисел более вероятен? Поясните свое мнение.
Предполагаемый ответ - оба набора имеют одинаковую вероятность выигрыша. Как это обосновать? Хочется предостеречь учителя от попытки сослаться на частоту. Хотя частотный подход является в учебнике основным, здесь он не работает. Дело в том, что в условиях данной лотереи существует
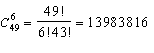
различных исходов. Поэтому даже теоретически невозможно вообразить такое количество тиражей, после которого можно будет сделать статистический вывод об их равновероятности. В данной ситуации она следует лишь из наших предположений о справедливом устройстве лотереи, ее симметрии (если, конечно, у нас нет оснований подозревать ее организаторов в обмане). Задача хорошо иллюстрирует границы частотного подхода и показывает, что иногда предположения о распределении вероятностей можно вывести только из рассмотрения природы самого объекта, <производящего> случай (равно как в опыте с кнопками на с. 393 - только из статистических данных). По поводу игры в подобного рода лотереи можно вспомнить остроумное замечание Мартина Гарднера - лучше делать ставку на <регулярные> комбинации. Их шансы на выигрыш те же, а сумма предполагаемого выигрыша в среднем больше, так как никому другому не придет в голову зачеркнуть номера 1, 2, 3, 4, 5, 6, и вам не придется делить призовой фонд с кем-то еще.
Таким образом, можно повысить
математическое ожидание суммы
выигрыша подчеркнем еще раз, что
вероятность угадать 6 номеров
остается прежней -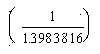
.
1273. У Юры в коробке 25 белых и 50 красных шаров, у Наташи в коробке 40 белых и 80 красных шаров. Они играют в игру, победителем которой становится тот, кто первым, не глядя, вынет белый шар из своей коробки. Если они вынимают белый шар одновременно - ничья. Юра считает, что эта игра несправедливая, так как у него в коробке меньше белых шаров. Согласны ли вы с Юрой? Наташа считает, что эта игра несправедливая, так как у Юры лучше отметки по математике и он лучше знает теорию вероятностей. Согласны ли вы с Наташей?
В этой почти шуточной задаче учителя ожидает любопытный подвох. В условии не совсем точно описан механизм вытаскивания шаров (вот он - тот самый признак проблемности!): можно возвращать вынутый шар в урну, а можно нет. В теории вероятностей это две хорошо известные <урновые схемы>.
В первом случае шансы игроков
одинаковы. На каждом шаге
вероятность вытащить белый шар для
любого из них 
, а значит, шансы на
победу во всей партии у них равны.
Гораздо сложнее обстоит дело во
втором случае. Если шары вынимаются
без возвращения, то после каждого
шага соотношение белых и красных
шаров в урнах меняется. На первом
шаге вероятность вытащить белый
шар для того и другого љљ.
Если на первом шаге ни один из них этого не сделал, то на втором более выгодное положение у Юры, так как в его урне соотношение шаров 25:49, а у Наташи 40:79. После каждого следующего шага это неравенство шансов только усугубляется.
Чтобы избавиться от громоздких вычислений, изменим условие задачи: пусть у Юры в коробке всего 1 белый и 2 красных шара. Тогда его мнение выглядит еще более <обоснованным> (в его коробке всего один белый шар). Он может одержать победу на первом, втором или третьем шаге (других вариантов нет):
1) Юра: Б 2) Юра: КБ 3) Юра: ККБ Наташа: К љљљљНаташа: КК љНаташа: ККК
Отсюда вероятность его победы будет
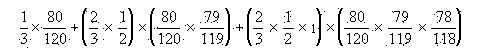= 0,47.
Аналогично можно рассчитать вероятность выигрыша Наташи - она будет 0,30, а вероятность ничьей - 0,23. Как видим, именно у Юры шансы почти в полтора раза больше (хотя в его коробке меньше белых шаров!).
Вернемся к условию нашей задачи, но для расчетов воспользуемся компьютером. В результате соотношение шансов получится 400:202:398. Неудивительно, что они почти выравниваются, поскольку с увеличением числа шаров две урновые схемы становятся эквивалентными, но у Юры шансы все равно будут выше. Нужно ли учителю специально выводить учащихся на схему без возвращения? Думаю, что это зависит от подготовки школьников. Но в любом случае он должен быть готов к этому вопросу - знать точный ответ и уметь хотя бы качественно объяснить неравенство шансов: доля белых шаров у Юры возрастает быстрее в процессе продолжения партии.
1276. Ребята провели опыты по подбрасыванию монеты. Из 100 раз <орел> выпал 46 раз, <решка> 54 раза. Ребята поспорили, что вероятней появится при следующем бросании: <орел> или <решка>? <Вероятней появление <орла>, - сказал Егор, - ведь до этого эксперимента он выпадал реже, чем решка, значит, теперь должен выпадать чаще>.
<Вероятней появление <решки>, - сказал Лева, - раз она выпадала чаще, то и будет выпадать чаще>. <Появление <орла> и <решки> равновероятно, - сказала Наташа, - так как результат каждого следующего случайного эксперимента не зависит от результатов предыдущих>.
С кем бы вы согласились и почему?
Мнение Егора - типичная <бытовая> трактовка закона больших чисел. О нем слышали даже люди, далекие от математики. В самой общей формулировке он гласит, что частота стремится к вероятности с увеличением числа опытов (не будем здесь уточнять, при каких условиях и в каком смысле <стремится> - не это здесь главное), то есть,
если N - число испытаний, No - число орлов, Np - число решек, то
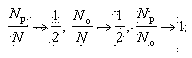
Но в том-то и дело, что только отношение стремится к 1. При этом разность Np - No может оставаться сколь угодно большой! Например, после 1000 бросаний эта разность, равная 8 после 100 бросаний, может сохраниться, а отношение станет намного ближе к 1:
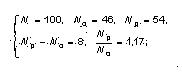
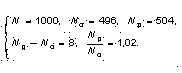
Таким образом, из утверждения, что
частота стремится к 
, не следует,
что Np - No должно стремиться к нулю,
поэтому орлы не обязаны в
дальнейших бросаниях выпадать чаще
решек - <у монеты нет памяти>. Мнение Левы, как ни странно,
довольно разумно. Основанием для
него может служить подозрение, что
реальная монета не симметрична
(вспомним, что все эти задачи из
раздела <Вероятность вокруг нас>); вероятности орла и решки
для нее могут отличаться от .
Посмотрим, можно ли эти подозрения подкрепить расчетами. Найдем вероятность того, что правильная монета при 100 бросаниях выпадет на решку не менее 54 раз:
(здесь Ф - функция Лапласа - см., например, [2]). Как видим, вероятность значительная, поэтому особых оснований для подозрений нет - в 20% случаев правильная монета будет вести себя также или еще хуже. А вот если после 100 бросаний мы получили бы Np = 75, то
и все основания согласиться с Левой у нас, пожалуй, имелись бы. Как видим, предположение о равновероятности можно пересматривать по результатам испытаний, - если для этого есть достаточные основания. Можно предложить на эту тему такой эксперимент: каждый ученик проводит со своей монетой 100 испытаний и делает после этого заключение о ее правильности. Затем они обмениваются монетами (например, попарно) и оценивают точно так же чужую.
Интересно сравнить результаты <экспертных> оценок одной и той же монеты. Разумеется, при обсуждении мнения Левы с учениками 6-го класса не надо объяснять им, что такое функция Лапласа, но сказать, что искомую вероятность можно вычислить и что кое-кто из них потом научится это делать, совсем не лишне. И даже записать, чему она равна.
Все это очень важно даже на качественном уровне - школьники уже в 6-м классе начинают понимать, вероятность каких событий надо посчитать, чтобы ответить на поставленный вопрос. Это и есть воспитание вероятностной культуры, о чем не раз говорили авторы [1] в своих выступлениях перед учительской аудиторией.
Но мы забыли о последнем мнении - Наташином. Предположение о равновероятности обосновывается в нем независимостью испытаний. В теории вероятностей эти два понятия вообще никак не связаны между собой - достаточно вспомнить опыт с кнопками, где испытания независимы, а равновероятности нет. С другой стороны, можно понять, что имеет в виду Наташа - поясним это на примере урновой схемы.
Будем без возвращения вынимать
шары из урны, в которой 100 белых и 100
красных шаров. Вероятности
появления на 101-м шаге белого и
красного шаров, разумеется,
одинаковы (в силу все той же
симметрии). Но пусть теперь нам
известно, что после 100 испытаний мы
получили 46 белых и 54 красных шара.
Тогда вероятность появления в 101-м
испытании белого шара больше - она
равна 
.
Дело в том, что здесь мы имеем дело
с двумя вероятностями: безусловной 
љи
условной
љ . В опыте с монетой они
равны, так как испытания
независимы, а в этом опыте они не
равны, поскольку испытания
зависимы. Значит, Наташа права в том
смысле, что вероятности появления
орла или решки в 101-м испытании
будут те же, что и в первом, но из
этого не следует, что эти
вероятности равны љ(все равно
нужна ссылка на симметрию монеты!).
Обсуждение этого мнения со
школьниками может занять много
времени, но послужит хорошей
подготовкой к введению в
дальнейшем понятий независимых
событий и условной вероятности.
1279.љЖеня купил булочку с изюмом, но изюма в ней не оказалось. Стоит ли Жене подавать в суд на хлебопекарный завод?
Первый вопрос, который можно здесь обсудить, - почему событие A = {в купленной Женей булке нет изюма} можно считать случайным?
Во-первых, по-видимому, изюм попадает в булку случайно: его бросают в тесто перед выпечкой и затем перемешивают. Даже при тщательном перемешивании в какие-то булки он может не попасть.
Во-вторых, из всей совокупности
выпеченных булок Женя выбирает
свою случайно. Чтобы говорить о
вероятности интересующего нас
события A, нужно знать, сколько
всего было булок и изюма при
выпечке. Если, скажем, на 1000 булок
полагалось 500 изюминок, то при самом
тщательном перемешивании по
крайней мере 500 булок останутся без
изюма (скорее всего, их будет
намного больше). Таким образом, в
этом случае вероятность события А
больше , и у Жени не будет никаких
оснований жаловаться не только на
хлебозавод, но и на судьбу.
Теперь возьмем случай более реальный: на 1000 булок полагалось 10000 изюминок - т. е. в среднем по 10 изюминок на булку. Какова в этом случае вероятность события А?
Для точного ее вычисления нам
опять понадобятся математические
основы вероятности. Любой
математик (а во Франции, кстати
говоря, даже старшеклассник!) сразу
скажет, что здесь мы имеем дело со
схемой Бернулли, где количество
испытаний N = 10000, а вероятность
успеха pљ=
љ (успех - очередная из 10000
изюминок попадает в Женину булку).
Правда, испытания можно считать
лишь приближенно независимыми, так
как если в булку уже попало 5000
изюминок, то для остальных там
просто не будет места. Но поскольку
вероятности таких событий очень
малы, то про эту зависимость можно
забыть и найти вероятность
интересуещего нас события как
(если наш математик еще и <вероятностник>, то он
сразу перейдет к пуассоновскому
приближению с параметром љ
љи
найдет эту вероятность как 
).
Казалось бы, полученная вероятность очень мала, и у Жени есть основания жаловаться, но, -љскорее на судьбу, чем на хлебозавод. Дело в том, что булок-то в выпущенной партии 1000, поэтому вероятность, что среди них есть хотя бы одна без изюма, будет (опять же приближенно)
.
Если каждый, кто окажется
на месте Жени, будет подавать в суд,
то вероятность не получить жалобу
равна 0,95. Однако булки пекутся
каждый день, поэтому вероятность
проработать весь год без жалоб есть
Событие практически невозможное! Получается, что у хлебозавода в этом случае нет никаких шансов на спокойную работу. Так что в суд Жене подавать не стоит. А что делать, если он купил три булки и все они оказались без изюма? Вообще, сколько таких булок он должен купить, чтобы понять, наконец, что изюм все-таки воруют? Все эти вопросы хорошо разобраны в книгах [3], [4], к которым мы и отсылаем читателя. Книга [3], кстати говоря, содержит методические рекомендации по преподаванию вузовского курса вероятности, в которых школьный учитель тоже найдет для себя много интересного.
При обсуждении этой задачи со школьниками можно устроить <следственный эксперимент>, то есть смоделировать эту случайную ситуацию. Методика таких экспериментов подробно описана в прекрасной книге [5], где через них школьники 5-6 классов могут познакомиться с такими понятиями, как испытания Бернулли, распределение Пуассона и т.д. Отметим также удачную идею авторов [5] использовать в качетсве генератора случая таблицу случайных чисел, что позволяет ставить случайные эксперименты любой степени сложности.
Литература
1. Математика-6. Учебник для общеобразовательных учебных заведений под редакцией Г.В. Дорофеева и И.Ф. Шарыгина.- М., Просвещение, 1995.
2. В.Феллер. Введение в теорию вероятностей и ее приложения.-М., ИЛ, 1952.
3. В.Н.Тутубалин. Теория вероятностей.- М., Изд-во МГУ, 1972.
4. В.Н.Тутубалин. Теория вероятностей и случайных процессов.-М., Изд-во МГУ, 1992.
5. М.Глеман, Т.Варга. Вероятность в играх и развлечениях.-М., Просвещение, 1979.
P.S. Автор будет рад продолжить обсуждение затронутых в статье проблем со всеми заинтересованными читателями. Можно писать по адресу:
248023 Калуга, ул. Ст.Разина, 26, Калужский педагогический университет, кафедра алгебры и информатики, Булычеву Владимиру Александровичу. љE-mail: bul@kgpu.kaluga.su