Курс стереометрии общеобразовательной школы по программе, рассчитанной на два урока в неделю, страдает в своей практической части недостаточной преемственностью курса планиметрии, слабой взаимосвязью с другими учебными предметами и не является в полной мере составной частью базы знаний, необходимых учащимся для продолжения образования в высших учебных заведениях.
Метод сечений, широко известный своей универсальностью, применяется РІ некоторых разделах физики, РІ теоретической механике, сопротивлении материалов, гидравлике, РІ некоторых разделах высшей математики Рё РґСЂСѓРіРёС… естественных науках Рё технических дисциплинах высшего образования. Ртот метод оказывает значительное влияние РЅР° развитие Сѓ учащихся пространственных представлений Рё пространственного мышления.
Данный материал характеризуется следующими особенностями:
1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
2. В задачах используются в основном простейшие многогранники - с целью доступности решения таких задач как учащимися, так и учителями, а также ввиду возможности применения одних и тех же геометрических конструкций по нескольку раз для изучения различных тем.
3. Учителям, знакомящимся с данным материалом, предлагается самим оценить уровень его трудности в соответствии с уровнем подготовки своих учащихся. Материал как полностью, так и частично, может быть полезен классам и школам всех типов, в том числе и классам с углубленным изучением математики.
4. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного применения. В некоторых задачах намеренно повторяются алгоритмы вычисления различных элементов с целью упрочнения умений и навыков учащихся и стандартизации подхода к решению предложенных и аналогичных задач.
Материал расположен в той последовательности, в какой он применялся для обучения учащихся. Классифицировать его по тематике задач с примерным соблюдением принципа «от простого к сложному» можно весьма условно следующим образом:
I. Нахождение площади сечений в многогранниках (до изучения теоремы о площади ортогональной проекции многоугольника).
II. Рспользование свойств подобных треугольников.
III. Нахождение расстояния и угла между скрещивающимися прямыми в многогранниках.
IV. Определение угла между плоскостями.
V. Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).
VI. Отношение объемов частей многогранника.
VII. Наибольшее и наименьшее значения площади переменного сечения в многогранниках.
VIII. Вращение многогранников.
Применение метода сечений в практической части большинства тем стереометрии подтверждает его универсальность.
Тема I.
(до изучения теоремы о площади ортогональной проекции многоугольника)
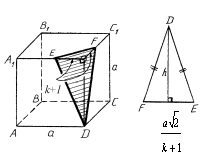
1. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершину D и точки E и F на ребрах A1D1 и C1D1 соответственно, если A1E = k•D1E и C1F = k•D1F.

DE =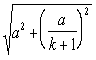 .
.
В сечении - равнобедренный треугольник DEF.
h = 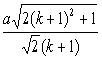 .
.
Ответ:
Sсеч.= SDDEF
=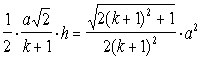 .
.
Возможные варианты:
k = 0 Ю Sсеч. =![]() (равносторонний DA1C1D);
(равносторонний DA1C1D);
k = 1 Ю Sсеч.=![]() ; k =
2 Ю Sсеч. =
; k =
2 Ю Sсеч. =![]() ;
;
k = 3 Ю Sсеч. = ![]() ; k =
4 Ю Sсеч. =
; k =
4 Ю Sсеч. = ![]() ;
;
k = 6 Ю Sсеч. =![]() ; k
= 1,5 Ю Sсеч. =
; k
= 1,5 Ю Sсеч. = ![]() ;
;
k = 0,5 Ю Sсеч. = ![]() ; k
= 0,1 Ю Sсеч. =
; k
= 0,1 Ю Sсеч. = 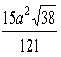 .
.
2. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершины C1 и D и точку E на ребре A1D1, если A1E = k•D1E.
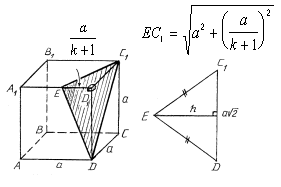
В сечении - равнобедренный треугольник C1DE.
.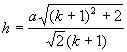
Ответ:
Sсеч. =SDC1DE
=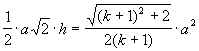 .
.
Возможные варианты:
k = 1 Ю Sсеч. = ![]() ; k
= 2 Ю Sсеч. =
; k
= 2 Ю Sсеч. =![]() ;
;
k = 3 Ю Sсеч. = ![]() ; k
= 4 Ю Sсеч. =
; k
= 4 Ю Sсеч. = ![]() ;
;
k = 0,75 Ю Sсеч. = ![]() ;
;
k = 0,4 Ю Sсеч.. = 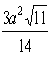 .
.
3. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершину D и точки E и F на ребрах A1D1 и D1C1 соответственно, если D1E = k•A1E и C1F = k•D1F.
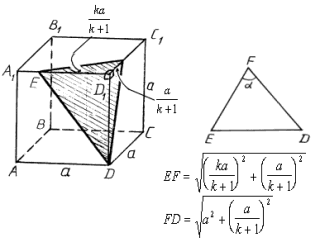
В сечении - произвольный треугольник DEF.
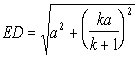 .
.
Алгоритм нахождения площади треугольника по трем сторонам, выраженным неравными иррациональными числами:
1) для стороны DE по теореме косинусов
DE2 = EF2 + DF2 – 2•EF•DF•cos a Ю
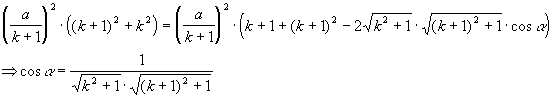 ;
;
2) 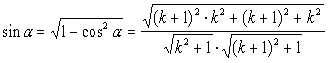 ;
;
3) Sсеч. = SDDEF =![]()
Возможные варианты (k № 0 и k № 1):
k = 2 Ю Sсеч. =![]() ; k
= 3 Ю Sсеч. =
; k
= 3 Ю Sсеч. = ![]() ;
;
k = 5 Ю Sсеч. = ![]() ; k =
1,5 Ю Sсеч. =
; k =
1,5 Ю Sсеч. = ![]() .
.
4. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершины A1 и C1 и точку F на ребре AD, если AF = k•DF.
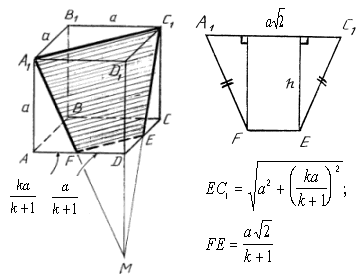
Сначала устанавливаем вид фигуры.
FE || A1C1 (методом «от противного»); затем, переходя от подобия DA1D1M и DFDM к подобию DC1D1M и DEDM, устанавливаем, что DF = DE.
Можем не строить т. M, а доказать, что FE || A1C1, применив теорему о двух параллельных плоскостях, пересеченных третьей плоскостью; затем, применив теорему о двух прямых, параллельных третьей (AC || A1C1 и FE || A1C1 Ю FE || AC), можем рассмотреть подобие DACD и DFED.
В результате получим DF = DE Ю AF = CE Ю DAA1F = DCC1E (по двум катетам) Ю A1F = C1E.
В сечении - равнобокая трапеция.
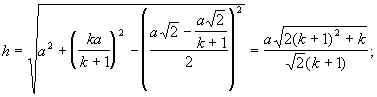
Sсеч. = SA1C1EF
= 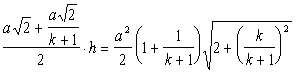 .
.
Возможные варианты:
k = 1 Ю Sсеч. = ![]() ; k = 2 Ю Sсеч. =
; k = 2 Ю Sсеч. = ![]() ;
;
k =![]() Ю Sсеч. =
Ю Sсеч. =![]() ; k
=
; k
=![]() Ю Sсеч. =
Ю Sсеч. =![]() ;
;
k =![]() Ю Sсеч. =
Ю Sсеч. = ![]() ; k
=
; k
=![]() Ю Sсеч. =
Ю Sсеч. =![]() .
.
5. Найти площадь сечения правильной четырехугольной пирамиды ABCDM с ребрами а (половинка октаэдра) плоскостью, проходящей через сторону основания AD и точку E на боковом ребре MC, если CE = k•ME.
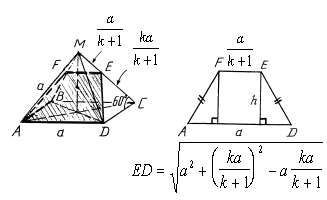
Сначала обосновываем EF || AD («от
противного») Ю DMEF
- равносторонний Ю EF =![]() ;
затем находим DE из DCDE по
теореме косинусов (и аналогично - AF).
;
затем находим DE из DCDE по
теореме косинусов (и аналогично - AF).
В сечении - равнобокая трапеция.
Ответ: Sсеч. = SAFED = ![]() .
.
Возможные варианты:
k = 1 Ю Sсеч.= ![]() ; k
= 2 Ю Sсеч. =
; k
= 2 Ю Sсеч. = ![]() ;
;
k = 4 Ю Sсеч.= ![]() ; k
=
; k
= ![]() Ю Sсеч. =
Ю Sсеч. = ![]() .
.
6. Найти площадь сечения правильного тетраэдра ABCM с ребром а плоскостью, проходящей через точки D, E и F на ребрах MA, MB и BC соответственно, если MD : AD = ME : BE = BF : CF = k.
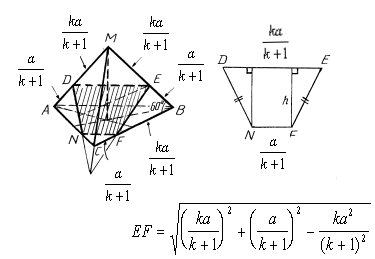
В сечении - равнобокая трапеция.
Ответ: Sсеч. = SDEFN = ![]() .
.
Возможные варианты:
![]() Ю Sсеч.=
Ю Sсеч.=![]() ;
;
![]() Ю Sсеч. =
Ю Sсеч. = ![]() ;
;
![]() Ю Sсеч. =
Ю Sсеч. = ![]() ;
; ![]() Ю Sсеч. =
Ю Sсеч. = ![]() ;
;
![]() Ю Sсеч. =
Ю Sсеч. =![]() ; k
= 1 Ю Sсеч. =
; k
= 1 Ю Sсеч. = ![]() (квадрат).
(квадрат).
7. Найти площадь сечения правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через сторону основания A1B1 и точку D на стороне BC другого основания, если CD = k•BD, сторона основания призмы равна а и высота H = na.
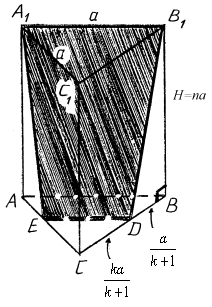
В сечении - равнобокая трапеция.
Ответ:
Sсеч. = 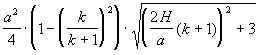 .
.
Для подбора вариантов удобно назначить
n = ![]() Р®
Р®
Ю Sсеч. = 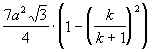 .
.
8. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершину C1 и середины ребер A1D1 и CD.
DF =![]() (находим из подобия).
(находим из подобия).
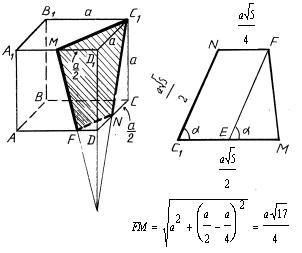
В сечении - неравнобокая трапеция.
РР· DMEF РїРѕ теореме
косинусов определяем cos a=![]() ,
,
затем sin a = ![]() ;
;
Sсеч. = SС1NFM = ![]() sin a=
sin a= ![]() .
.
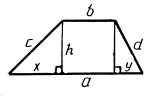
Приведем другой способ нахождения площади неравнобокой трапеции, стороны которой не являются рациональными числами:
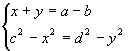 Р®
Р® 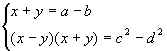 Р®
Р® 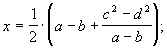
h = ![]() ; Sтрап. =
; Sтрап. = ![]() Чh.
Р§h.
Аналогичная задача с изменением условия:
D1M = 3Р§A1M.
В этом случае D1M =![]() Ю
DF =
Р®
DF =![]() ; Sсеч. =
; Sсеч. = ![]() .
.
9. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершины B1 и D и середину ребра CC1.
В сечении - ромб.
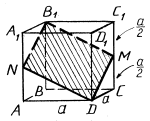
Ответ:
Sсеч. =SB1MDN
= ![]() ЧB1DЧMN
=
ЧB1DЧMN
= ![]() B1DЧAC =
B1DЧAC = ![]() .
.
10. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершины B1 и D и точку M на ребре CC1, если C1M = 2•CM.
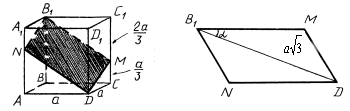
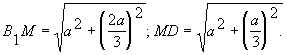 .
.
В сечении - параллелограмм.
РР· DB1DM РїРѕ
теореме косинусов находим cos a=![]() ,
затем sin a=
,
затем sin a=![]() ;
;
Sсеч. =SB1MDN = B1DЧB1MЧsin a =![]() .
.
Аналогичная задача с изменением условия:
C1M = 3Р§CM.
Тогда Sсеч.=![]() .
.
11. Найти площадь сечения куба ABCDA1B1C1D1 с ребром а плоскостью, проходящей через вершину B1 и середины ребер AD и CD.
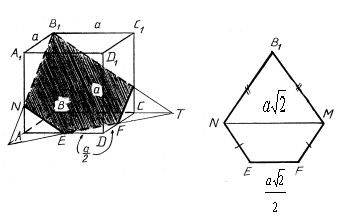
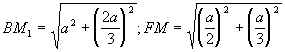 .
.
В сечении - пятиугольник.
Так как DDEF =DCTF,
то CT = ![]() ; затем из подобия DBB1T и DCMT
определяем CM =
; затем из подобия DBB1T и DCMT
определяем CM =![]() Ю C1M
=
Р® C1M
=![]() ;
;
MN = AC = ![]() ; пятиугольник состоит из
равнобокой трапеции и равнобедренного
треугольника;
; пятиугольник состоит из
равнобокой трапеции и равнобедренного
треугольника;
Sсеч. = ![]() .
.
Примечание к задаче 11. Пятиугольник можно достроить до ромба.
12. В правильной треугольной призме ABCA1B1C1 со стороной основания а и высотой H=na найти площадь сечения призмы плоскостью, проходящей через вершину C и середины ребер AA1 и A1B1.
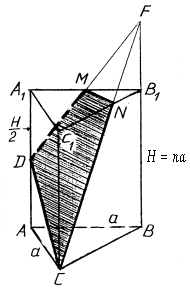
В сечении - произвольный четырехугольник.
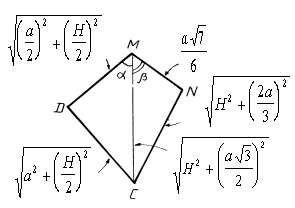
Так как DA1DM = DB1FM, то B1F = ![]() ;
затем из подобия DBCF и DB1NF определяем B1N
=
;
затем из подобия DBCF и DB1NF определяем B1N
=![]() Р® C1N =
Ю C1N =![]() . Отрезок MN
находим из DMNB1 по
теореме косинусов; диагональ CM можно найти
из прямоугольного треугольника CC1M (на
рисунке не показан). Площадь четырехугольника CDMN
определяем по сумме площадей треугольников CDM
и CMN, введя вспомогательные углы a
Рё b.
. Отрезок MN
находим из DMNB1 по
теореме косинусов; диагональ CM можно найти
из прямоугольного треугольника CC1M (на
рисунке не показан). Площадь четырехугольника CDMN
определяем по сумме площадей треугольников CDM
и CMN, введя вспомогательные углы a
Рё b.
SDCDM = 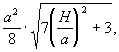 SDCMN =
SDCMN = 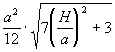 ;
;
Sсеч. =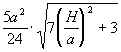 .
.
Возможные варианты:
n =![]() = 1 Ю Sсеч.
=
= 1 Ю Sсеч.
= ![]() ; n =
; n = ![]() Ю Sсеч.
=
Ю Sсеч.
=![]() ;
;
n =![]() Ю Sсеч. =
Ю Sсеч. =![]() .
.