А. Смоляков,
г. Нефтекумск

Выпускная экзаменационная работа в 1997/98

Вариант N 4-98

1. Решить уравнение

.

Решение. Данное уравнение равносильно системе

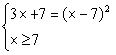
Решим уравнение системы:

3x + 7 = x² - 14x + 49,  x² – 17x + 42 = 0,

D = 289 - 168 = 121 > 0,

x_1,2 = , откуда x1 = 14, x2 = 3.

Условию x і 7 удовлетворяет первый корень, второй корень не удовлетворяет условию x і 7 и является посторонним для исходного уравнения.

Ответ: 14.

Замечание 1. Покажем еще один способ решения данного уравнения. Пусть t, где t  і 0, тогда
x = и данное уравнение примет вид

t = – 7,  t² – 3t – 28 = 0, D = 9 + 112 = 121 > 0,

t_{1,2 =}  , t₁ = 7, t₂ < 0.

Следовательно, остается решить уравнение7, откуда 3x + 7 = 49, откуда x = 14.

Замечание 2. Оформление решения данного уравнения можно представить и в таком виде:

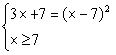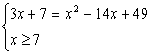
x - 7 Ы  Ы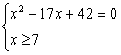

Ы Ы откуда x = 14.

Замечание 3. Укажем и самый стандартный прием решения рассматриваемого уравнения. Возведем обе части уравнения в квадрат, получим 3x + 7 = (x - 7)², откуда x² - 14x + 49 = 3x + 7, x² - 17x + 42 = 0. По теореме Виета (x₁ + x₂ = 17, x₁x₂ = 42) находим, что x₁ = 14, x₂ = 3.

Проверка.

x = 14, = 7 - равенство верное, 14 - корень данного уравнения.

x = 3, = - 4 - равенство ложное, 3 - не корень данного уравнения.

Ответ: 14.

2. Решить уравнение 14sin² x + cos 4x - 10 = 0.

Решение. Так как

sin² x = и cos 4x = 2cos² 2x - 1,

то данное уравнение равносильно уравнению

7(1 - cos 2x) + 2cos² 2x - 1 - 10 = 0,

2cos² 2x - 7 cos 2x - 4 = 0.

Положим cos 2x = y, где | y | Ј 1, тогда 2y² - 7y - 4 = 0.
D = 49 + 32 = 81 > 0, y_1,2 = , y₁ = 4, y₂ = - . Условию | y | Ј 1 удовлетворяет только второй корень, поэтому необходимо решить уравнение cos 2x = - , откуда

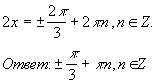
Замечание. Наметим и другой вариант решения уравнения. Так как cos 4x = 1 - 2sin² 2x, то данное уравнение примет вид

14sin² x - 8sin² x cos² x - 9 = 0

или

14sin² x - 8sin² x + 8sin⁴ x - 9 = 0,

8sin⁴ x + 6sin² x - 9 = 0.

Далее остается ввести новое неизвестное: sin² x = y, где yО (0; 1).

3. Вычислить .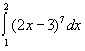

Решение. Функция f(x) = (2x - 3)⁷ непрерывна и интегрируема на отрезке [1; 2] как многочлен. Применяя формулу Ньютона–Лейбница, получим

=.

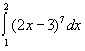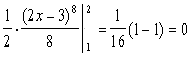Ответ: 0.

4. Решить неравенство  .

Решение. Так как D(log_a) = R₊, где a > 0, a № 1, то
x² - 2x - 9 > 0, x + 1 > 0. Так как > 1, то функция

возрастающая и x² - 2x - 9 і x + 1. Следовательно, данное неравенство равносильно системе

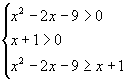
которая равносильна системе

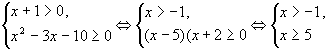
откуда x і 5.

Замечание 1. Решая систему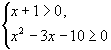 можно дать ее подробное решение. Решим второе неравенство методом интервалов. f(x) = x² - 3x - 10, D(f) = R, так как f - многочлен. Найдем нули функции: x² - 3x - 10 = 0,
D = 9 + 40 = 49 > 0.

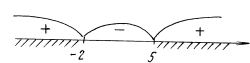
Находим общее решение системы:

Ответ: [5; +Ґ ).

Замечание 2. При выполнении этого задания иногда решавшие его находили так называемую ОДЗ, что в данном примере приводит к усложнению решения: ведь необходимо тогда решить и неравенство x² - 2x - 9 > 0.

Замечание 3. Данное неравенство можно решить методом интервалов. Пусть

f(x) = log_p/3(x² - 2x - 9) - log_p/3(x + 1).

Необходимо найти все x, при которых f(x) і 0. Находим D(f):

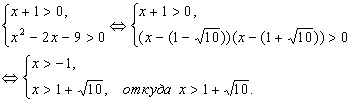
Итак, D(f) = . Находим нули f: x² - 3x - 10 = 0, откуда x = - 2 - не нуль функции, так как
- 2П , x = 5 - нуль функции.

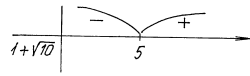
f(6) =  log_p/315 -  log_p/37 > 0,

f(4,5) =  log_p/32,25 - log_p/35,5 < 0.

5. Найти наибольшее и наименьшее значения функции f(x) = tg x - x на отрезке .

Решение. Заданная функция определена и непрерывна на отрезке и дифференцируема на интервале . Найдем производную функции f(x):

f '(x) = 1/cos² x - 1 = 1 + tg² x - 1 = tg² x.

Так как f '(x) і 0 при всех x из промежутка , f(x) = 0 лишь при x = p и f(x) непрерывна на , то функция монотонно возрастает на и свое наименьшее значение принимает на левом конце отрезка, а наибольшее - на правом. Далее имеем:

- наименьшее значение функции,
- наибольшее значение функции.

Ответ:  на   min f(x) == ,   max  f(x) == .

Замечание. Задачу можно решить, применив алгоритм нахождения наибольшего и наименьшего значений функции на отрезке. Мы нашли, что f '(x) = tg² x. Найдем критические точки: tg² x = 0, x =pn, nОZ. Выберем из них те, которые принадлежат отрезку . Для этого решим неравенство 3p/4< pn <5p/4 , nОZ.
Имеем 3/4< n <5/4 , откуда n = 1 и x = p. Вычисляем значение функции на концах отрезка и в полученной критической точке:

=, f(p)=-p , =.

Дальнейшие рассуждения очевидны:

4 > p Ю 4 + 3p > 4p Ю   < – p,

p < 4 Ю 5p < 4 + 4p Ю 5p – 4 < 4p Ю > – p.

6. При каком значении a графики функций

y = ln (3x – 4) и y = 3x – 4 + a

имеют единственную общую точку?

Решение. Введем новую переменную, положив 3x – 4 = t, где t > 0. Тогда необходимо выяснить, при каком значении a графики функций y₁ = ln t и y₂ = t + a имеют единственную общую точку. Обозначив абсциссу общей точки через x0, получим ln t₀ = t₀ + a. Так как графики имеют единственную общую точку, то прямая y₁ = t + a является касательной к графику функции y₂ = ln t в точке с абсциссой t₀, а поэтому y₁' = y₂' и при t=t₀ ln' t = 1, откуда 1/t₀= 1, t₀ = 1, a = ln t₀ – t0 = – 1. Покажем, что прямая y = t – 1 не имеет других общих точек с графиком функции y = ln t, отличных от точки (1; 0). С этой целью докажем неравенство t – 1 > ln t (при t > 0, t № 1). Введем функцию f(t) = t – 1 – ln t;  f '(t) = 1 –1/t . f '(t) > 0 при t > 1 и функция f(t) на промежутке [1; +Ґ) возрастает, а поэтому f(t) > f(1). f '(t) < 0 при 0 < t < 1 и функция на промежутке (0; 1] убывает, а поэтому f(t) > f(1). Итак, при t > 0 f(t) = t – 1 – ln t > f(1) = 0, т. е. t – 1 > ln t. Следовательно, при a = – 1 и графики данных функций имеют только одну общую точку.

Ответ: a = – 1.

Замечание 1. Анализ решенной задачи позволяет ее обобщить. Вместо функции 3x - 4 можно взять любую другую линейную функцию вида y = kx + b, где k № 0. Будут меняться только координаты общей точки, при этом ее ордината всегда равна 0.

Замечание 2. При решении задачи рассмотренным способом мы показали, что при найденном значении a действительно существует только одна общая точка. Это важно. Мы подробно остановимся на решении задачи N 6, так как практически во всех работах, которые мы увидели в медальной комиссии, рассматривался вариант приведенного нами решения с некоторыми усложнениями. При этом утверждалось, что функции y = 3x - 4 + a
и y = ln (3x - 4) - возрастающие, каждая в своей области определения, а поэтому их графики могут иметь две общие точки, одну или ни одной. Во втором случае y = 3x - 4 + a - касательная. На наш взгляд, решение верное, но потому, что y = ln (3x - 4) - функция выпуклая, возрастающая и не имеющая точек перегиба.

Замечание 3. Задача решается просто, если вновь ввести новое неизвестное t = 3x - 4, где t > 0, и сформулировать задачу так: «При каких значениях a уравнение ln t = t + a имеет единственный корень»? Перепишем уравнение: ln t - t = a и построим график функции f(t) = ln t - t, проведя исследования.

1. D(f) = R₊.

2. f '(t) =1/t - t. Критическая точка t = 1.

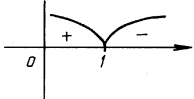
3. На промежутке (0; 1] функция возрастает, а на промежутке [1; +Ґ) функция убывает.

4. При x_max = 1 y_max = - 1.

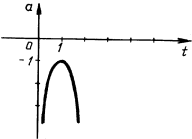
Ясно, что при a = - 1 уравнение ln t - t = - 1 имеет единственный корень t = 1.

Теперь делаем вывод, что графики функций

y = ln (3x - 4) и y = 3x - 4 + a

имеют единственную общую точку при a = - 1. Ее координаты .(5/3;0)