В этой статье мы постараемся показать
применение методов интервалов для решения
иррациональных, показательных, логарифмических
и других неравенств.
Универсальность метода интервалов заложена уже
в его содержании. Находим область определения
функции, затем отмечаем в этой области нули
функции, которые разбивают область определения
на несколько промежутков, внутри каждого из
которых функция определена, непрерывна и
сохраняет знак. Для определения знака функции на
конкретном промежутке находим знак в любой
(удобной) точке этого промежутка.
Рллюстрацию изменения знаков функции будем
осуществлять с помощью координатной прямой.
Естественно, что показ учащимся метода
интервалов для решения более широкого класса
неравенств можно давать после рассмотрения
традиционных приемов их решения.
Все рассматриваемые упражнения взяты из
вариантов вступительных экзаменов в различные
вузы страны.
Материал представляет, по мнению автора, интерес
для проведения факультативных занятий.
I. Примеры решения иррациональных неравенств
1. ![]() .
.
Решение. Введем функцию f(x) =![]() –
3. Необходимо определить промежутки, на которых f(x)Ј 0. Очевидно, что D(f) = [0;Ґ).
Нули f(x): x = 9.
–
3. Необходимо определить промежутки, на которых f(x)Ј 0. Очевидно, что D(f) = [0;Ґ).
Нули f(x): x = 9.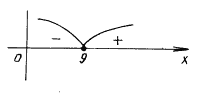
f(16) >0,
f(4) < 0.
Ответ: [0; 9].
2. ![]() < 2 – x.
< 2 – x.
Решение. Традиционное решение этого неравенства приводит к системе неравенств
Решение этого неравенства можно осуществить,
положив ![]() = y, где y і 0.
Получаем
= y, РіРґРµ y С– 0.
Получаем
y < 20 – y2, y2 + y – 20 < 0, (y + 5)(y – 4) < 0,
откуда y < 4, поскольку yі0.
Ртак, ![]() < 4 Рё – 18Р€ x Р€
–2.
< 4 и – 18Ј x Ј
–2.
Рнтересен Рё такой вариант (графический) решения
примера. Если заметить, что f(x) =![]() – функция
возрастающая на луче [– 18; +Ґ ),
а g(x) = 2 – x – убывающая на R и x
= 2 – абсцисса их точки пересечения и при этом f(– 14)
< g(– 14), то ясен и
– функция
возрастающая на луче [– 18; +Ґ ),
а g(x) = 2 – x – убывающая на R и x
= 2 – абсцисса их точки пересечения и при этом f(– 14)
< g(– 14), то ясен и
ответ: [– 18; – 2).
Обратимся к теме статьи. Пусть f(x) =![]() +
x – 2. Надо решить неравенство f(x)< 0.
Заметим, что D(f)=[– 18; +Ґ).
Нули функции найдем, решив уравнение
+
x – 2. Надо решить неравенство f(x)< 0.
Заметим, что D(f)=[– 18; +Ґ).
Нули функции найдем, решив уравнение ![]() = 2
– x, откуда x = – 2.
= 2
– x, откуда x = – 2.
Применяем метод интервалов: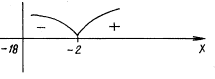
f(– 14) < 0,
f(7) > 0.
Ответ: [– 18; – 2).
3. ![]() < 20.
< 20.
Решение. Область допустимых значений определяется системой неравенств
.
Р® xС– 4.
Для функции f(x) = ![]() – 20 D(f) = [4; + Ґ). Далее находим нули f(x):
– 20 D(f) = [4; + Ґ). Далее находим нули f(x):
откуда x = 29 и x = 13 – посторонний
корень.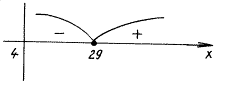
f(30) =![]() – 20 = 0,3 > 0,
– 20 = 0,3 > 0,
f(5) =![]() – 1 – 20 = – 10 < 0.
– 1 – 20 = – 10 < 0.
Ответ: [4; 29).
Примечание. Рто неравенство можно решить,
например, выполнив замену переменной ![]() = y,
РіРґРµ y С– 0.
= y,
РіРґРµ y С– 0.
4. ![]() < 1.
< 1.
Решение. Область определения функции f(x)
=![]() – 1 найдем, решив систему неравенств
– 1 найдем, решив систему неравенств
Легко видеть, что ![]() .
.
Находим нули функции f(x):
1 – 2x = ![]() , – 4x + 12x2 = 0,
x = 0 – посторонний корень, x =
, – 4x + 12x2 = 0,
x = 0 – посторонний корень, x =![]() ;
;
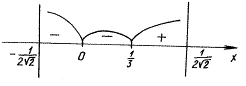
f(– 0,1) =![]() – 1 =
– 1 =![]() – 1 < 0,
– 1 < 0,
f(0,1) = ![]() – 1 =
– 1 =![]() < 0,
< 0,
f(0,34) =![]() – 1 =
– 1 = ![]() > 0.
> 0.
Ответ:![]() .
.
Примечание. Ртот пример показывает, что для РґРІСѓС… чисел, «близко» расположенных РЅР° координатной РїСЂСЏРјРѕР№, применение метода интервалов осуществимо.
5. ![]() >x – 1.
>x – 1.
Решение. Пусть f(x) = ![]() – x + 1. Найдем
область определения этой функции, для чего решим
неравенство x3 + x2 – 2x і
0 методом интервалов:
– x + 1. Найдем
область определения этой функции, для чего решим
неравенство x3 + x2 – 2x і
0 методом интервалов:
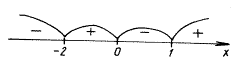
D(f) =![]() .
.
Рщем нули функции f, решив уравнение
![]() = x – 1, x3 = 1
Рё x = 1,
= x – 1, x3 = 1
Рё x = 1,
где x = 1 удовлетворяет уравнению, но не удовлетворяет исходному неравенству.
Далее применяем метод интервалов: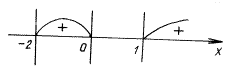
f(– 1) =![]() + 2 > 0,
+ 2 > 0,
f(2) = ![]() – 1 > 0.
– 1 > 0.
Ответ: ![]() .
.
Традиционное решение данного неравенства сводится к совокупности двух систем:
Примечание. Отметим, что не идет речь о преимуществах того или иного способа решения неравенств, а показывается применение метода интервалов на более широком классе неравенств.
Упражнения
Решите неравенства методом интервалов:
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
II. Примеры решения показательных неравенств
1. 4x < 2x+1 + 3.
Решение. Если f(x) = 4x – 2•2x – 3, то D(f) = R и необходимо решить неравенство f(x) < 0. Найдем нули
f: 4x–2•2x – 3 = 0, откуда 2x = 3, x = log23.
Далее применяем метод интервалов: 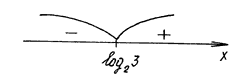
f(0) < 0, f(2) > 0.
Ответ: (– Ґ; log23).
2. ![]() – 3 Ј 0.
– 3 Ј 0.
Решение. Пусть f(x) =![]() – 3. Решаем
неравенство f(x)Ј 0. Заметим,
что D(f) = (– Тђ; 0)Р(0;
+ Ґ). Для нахождения нулей
функции f решаем уравнение:
– 3. Решаем
неравенство f(x)Ј 0. Заметим,
что D(f) = (– Тђ; 0)Р(0;
+ Ґ). Для нахождения нулей
функции f решаем уравнение:
![]() – 3 = 0.
– 3 = 0.
Полагая ![]() = t, где t > 0,
приходим к уравнению t2 –
= t, РіРґРµ t > 0,
приходим к уравнению t2 – ![]() t – 3 = 0 с
положительным корнем t = 2. Следовательно,
t – 3 = 0 с
положительным корнем t = 2. Следовательно, ![]() = 2
Рё x =
= 2
Рё x =![]() .
.
Применяем метод интервалов: 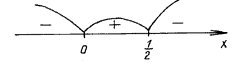
f(1) < 0,
f ![]() > 0,
> 0,
f(– 1) < 0.
Ответ: (– Ґ; 0) Р![]() .
.
3. 4x Р€![]() .
.
Решение. Рассмотрим функцию
f(x) = 4x – (![]() ) .
) .
Область определения функции f есть луч [0; + Ґ). Найдем теперь нули функции f:
4x – (![]() ) = 0.
) = 0.
Разделив обе части последнего уравнения на ![]() ,
получим
,
получим
![]() ,
, ![]()
откуда ![]() = 4, x–
= 4, x–![]() = 2, а это
уравнение имеет единственный корень x = 4.
= 2, а это
уравнение имеет единственный корень x = 4.
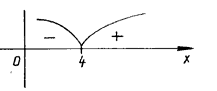
f(1) < 0, f(9) = 49 – 3•212 – 44 = 28(210 – 2•24 – 1) > 0.
Ответ: [0; 4].
4. ![]() < 1.
< 1.
Решение. Введем в рассмотрение функцию f(x) =![]() –
1. Легко видеть, что D(f) =
–
1. Легко видеть, что D(f) =![]() . Находим нули
функции f(x): 4x – 2 – 22x +
. Находим нули
функции f(x): 4x – 2 – 22x +![]() = 0.
Уравнение корней не имеет.
= 0.
Уравнение корней не имеет.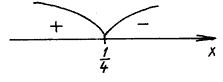
f(0) =![]() > 0,
> 0,
f(1) = ![]() < 0.
< 0.
Ответ: ![]() .
.
Упражнения
Решите методом интервалов неравенства:
5. 9x < 3x + 2.
6. ![]() .
.
7. ![]() .
.
8. 3•4x – 7•10x + 2•25x > 0.
9.![]() .
.
III. Примеры решения
логарифмических
неравенств методов интервалов.
1. lg2 x – 2lg x – 8 Ј 0.
Решение. f(x) = lg2 x – 2lg x – 8, D(f) = (0; + Ґ). Для нахождения нулей функции f решаем уравнение
lg2 x – 2lg x – 8 = 0,
откуда lg x = – 2, lg x = 4 и x =![]() , x = 10000.
, x = 10000. 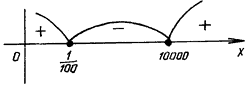
f(105) = 25 – 10 – 8 = 7 > 0,
f(1) < 0,
f(10–3) = 9 + 6 – 8 = 7 > 0.
Ответ: ![]() .
.
2. log0,3 (x2 – x – 20) – log0,3 (x + 4) > 0.
Решение. Найдем область определения функции f в левой части неравенства, решив систему неравенств
![]() Р® x > 5.
Р® x > 5.
Решая уравнение log 0,3 (x2 – x – 20) –
log0,3 (x + 4) = 0, находим нули функции f: x2
– x – 20 = x + 4, x2 – 2x – 24 = 0, x = – 4 –
посторонний корень и x = 6.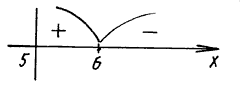
f(7) = log0,3 22 – log0,3 7 <0,
f(5,5) = log0,3 4,75 – log0,3 9,5>5.
Ответ: (5; 6).
3. ![]() .
.
Решение. Пусть f(x) = ![]() – 1. Необходимо
решить неравенство f(x) Ј 0.
– 1. Необходимо
решить неравенство f(x) Ј 0.
Область определения функции f определяется системой неравенств
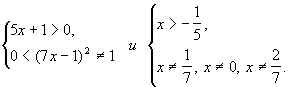
Ртак, D(f) = ![]() .
.
Найдем нули функции f:
log3 (5x + 1) = log3 (7x – 1)2,
откуда 49x2 – 19x = 0, x = 0 – посторонний
корень, x =![]() – корень уравнения.
– корень уравнения.
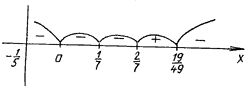
f(1) = ![]() < 0,
< 0,
f(0,3) = ![]() > 0,
> 0,
f(0,2) = ![]() – 1 < 0, так как log3 2
> 0, log3 0,4 < 0.
– 1 < 0, так как log3 2
> 0, log3 0,4 < 0.
f(0,1) =![]() < 0,
< 0,
f(– 0,1) =![]() < 0.
< 0.
Ответ: ![]() .
.
4. log3x+1![]() С– 0.
С– 0.
Решение. Для функции f(x) = log3x+1![]() находим область определения. Решаем систему
неравенств:
находим область определения. Решаем систему
неравенств:
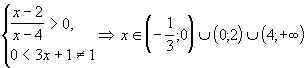 .
.
Найдем нули функции: log3x+1![]() = 0,
= 0, ![]() = 1,
но последнее уравнение корней не имеет.
= 1,
но последнее уравнение корней не имеет.
Применяем метод интервалов:
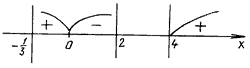
f(5) = log16 3 > 0,
f(1) = log4![]() < 0,
< 0,
f(– 0,2) = log0,4![]() > 0.
> 0.
Ответ: ![]() (4; + Ґ).
(4; + Тђ).
5. logx2 Р€ ![]() 2.
2.
Решение. Для функции f(x) = logx 2 – ![]() 2
имеем D(f) = (0; 1) Р(1; + Ґ). Очевидно, что для нахождения нулей f
необходимо решить уравнение x =
2
имеем D(f) = (0; 1) Р(1; + Ґ). Очевидно, что для нахождения нулей f
необходимо решить уравнение x =![]() , откуда x = 2.
, откуда x = 2.
Применяем метод интервалов:
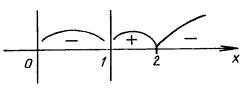
f(4) = log4 2 – log2 2 < 0,
f(1,5) =  ,
,
f = ![]() .
.
Ответ: (0; 1) Р[2; +Ґ).
Упражнения
Решите методом интервалов неравенства:
10. ![]()
11. log2 (x + 1) < 1 – 2log4 x.
12. ![]() .
.
13. logx![]() < 1.
< 1.
14. logx 3 Р€ log2x+3 9.
15. logx (1 – 2x) < 1.
16. log3 log27 log2 (x2 +
x + 2) Ј –1.
IV. Примеры на применение метода
интервалов
к неравенствам, содержащим знак модуля.
1. x2 > | 5x + 6 |.
Решение. Функция f(x) = x2 – | 5x +
6 | определена при любом x. Найдем ее нули,
решив уравнение
x2=| 5x + 6 |, откуда x2
= 5x + 6 или x2 = – (5x + 6), т. е.
x2 – 5x – 6 = 0 или x2 + 5x + 6 = 0.
Корни этих уравнений – 1, 6, – 2, – 3.
Далее применяем метод интервалов:
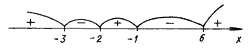
f(7) > 0, f(0) < 0, f(– 1,5) > 0, f(– 2,5) < 0, f(– 4) > 0.
Ответ: (– Ґ; – 3) Р(– 2; – 1) Р(6; + Ґ).
Примечание. Неравенство можно также решить, заменив его на равносильное (x2 – 5x – 6)(x2 + 5x + 6) > 0.
2. y2 – 4| y | < 12.
Решение. Здесь положим f(y) = y2 – 4| y | – 12. Заметим, что D(y) = R и найдем нули функции f: y2 – 4| y | – 12=0, откуда | y | = 6, | y | = – 2. Последнее уравнение корней не имеет.
Ответ: – 6 < y < 6.
3. ![]() .
.
Решение. Заменим неравенство на
равносильное 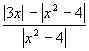 Ј 0 и
положим f(x) =
Р€ 0 Рё
положим f(x) =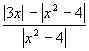 . Ясно, что D(f) = (– Ґ; – 2) Р(– 2; 2) Р(2; + Ґ). Находим нули
функции f, решая уравнение | 3x | = | x2
– 4 |, которое распадается на два:
. Ясно, что D(f) = (– Ґ; – 2) Р(– 2; 2) Р(2; + Ґ). Находим нули
функции f, решая уравнение | 3x | = | x2
– 4 |, которое распадается на два:
x2 – 3x – 4 = 0 и x2 + 3x – 4 = 0.
Корни этих уравнений соответственно равны – 1; 4 и 1; – 4.
Далее применяем метод интервалов:
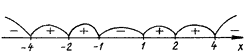
Ответ: (– Ґ; – 4] Р[ – 1; 1] Р[4; + Ґ).
Замечание. Конечно, при решении этого неравенства можно было учесть, что |x2 – 4 | > 0 при x№ ±2.
4. x2 + 2| x – 1 | + 7 Ј 4| x – 2 |.
Решение. Если f(x) = x2 + 2| x – 1 | + 7 – 4| x – 2 |, то D(f) = R и необходимо решить неравенство f(x) Ј 0.
Находим нули f:
Р°) 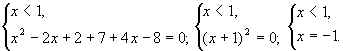
x = – 1 – нуль функции;
Р±) 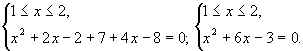
система решений не имеет;
РІ) 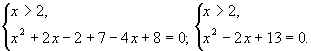
система не имеет решений.
Применяем метод интервалов:
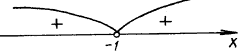
f(0) > 0,
f(– 2) > 0.
Ответ: – 1.
5.![]() + 3 > | x – 1 |.
+ 3 > | x – 1 |.
Решение. Для f(x) = ![]() + 3 – | x – 1 | находим D(f)
=
+ 3 – | x – 1 | находим D(f)
=![]() .
.
Находим нули функции f(x).
Если x![]() , то
, то
![]() +3 – x + 1 = 0,
+3 – x + 1 = 0, ![]() = x
– 4, 8x = 21,
= x
– 4, 8x = 21,
x = 2![]() – не корень.
– не корень.
Если x![]() , то
, то
![]() +3+x–1 = 0,
+3+x–1 = 0, ![]() =
– x – 2, 4x = – 9,
=
– x – 2, 4x = – 9,
x = – 2,25 – корень.
Ртак, функция f имеет РѕРґРёРЅ нуль x = –2,25.
Применяем метод интервалов:
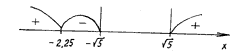
f(3) >0,
f(– 2,24) =![]() + 3 – 3,24 < 0,1 – 0,24 < 0,
+ 3 – 3,24 < 0,1 – 0,24 < 0,
f(– 3) > 0.
Ответ: (– Ґ; – 2,25) Р[5; + Ґ).
Упражнения
Решите методом интервалов неравенства:
17. | x – 6 | > x2 – 5x + 9.
18. 16| x2 – 2(x + | x | + 1 | < 1.
19. | x2 – | x + 1 || Ј 2x – 3.
20. ![]()
Ответы
| 1. (– Тђ; – 6] 2. 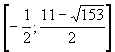 Р [0; 2). Р [0; 2). 3. (– Тђ; 0] Р [5; 7) Р (9; + Тђ). 4. [3; 4]. 5. (– Тђ; log3 2). 6. (– Тђ; 2) Р 7. [0; 16]. 8. 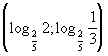 9. 10.[1;109]Р[1016;1025] |
11. (0;1) 12.[ 13.(0;1) 14. (0;1) Р (3;+Тђ) 15. 16.[-3;-1) Р (0;2) 17.(1;3) 18. 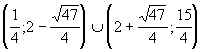 19. 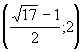 20. |
А. Смоляков,
г. Нефтекумск