Квадратный трехчлен и его свойства систематически изучаются в школьном курсе алгебры на протяжении нескольких лет. Задачи по этой теме – непременный атрибут экзамена по алгебре в школе и вступительного экзамена в вуз. Между тем, опыт показывает, что многие школьники усваивают этот материал формально и неглубоко, в результате чего легко попадают в ловушки, расставляемые «хитрыми» экзаменаторами. Цель настоящих заметок – разобрать несколько задач про квадратный трехчлен и рассказать о некоторых типичных ошибках, допускаемых школьниками при их решении. Материал может быть использован в полном объеме на уроках в 9 классе, хотя отдельные задачи доступны и восьмиклассникам.
Во-первых, следует помнить, что не всякое уравнение с параметром, внешне похожее на квадратное, является таковым при всех значениях этого параметра. Следует внимательно отслеживать те значения параметра, при которых обращается в нуль первый коэффициент уравнения: в этом случае уравнение вырождается в линейное, а известная формула для вычисления корней квадратного уравнения становится неприменимой.
Задача 1. Для каждого значения параметра d решить уравнение dx2 + 2x + 1 = 0.
Решение. а) Если d = 0, то получившееся
линейное уравнение 2x + 1 = 0 имеет единственный
корень
Если d№0, то квадратное уравнение dx2 + 2x + 1 = 0 с дискриминантом D = 4 – 4d:
– не имеет корней, если D < 0 Ы d > 1;
– имеет два различных корня 
если D > 0 Ы d < 1;
– имеет два совпадающих корня x1 = x2 = – 1, если D = 0 Ы d = 1.
Ответ: 
x1 = x2 = – 1, если d = 1;
нет решений, если d О (0; + Ґ).
Задача 2. При каких значениях параметра a уравнение
(a – 1)x2 + (a + 4)x – (a + 3) = 0 имеет два различных корня?
Решение. При a = 1 получаем линейное уравнение, имеющее только один корень.
При a № 1 получаем квадратное уравнение, наличие двух различных корней у которого равносильно положительности дискриминанта:
(a + 4)2 = (a + 1)(a + 3) > 0.
Решением этого неравенства является множество
из которого необходимо не забыть исключить значение a = 1.
Ответ: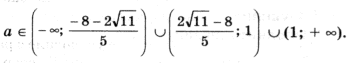 
Знак первого коэффициента квадратного трехчлена существенно влияет на его свойства. В этой связи часто бывает полезно рассмотреть по отдельности те множества значений параметра, на которых первый коэффициент трехчлена принимает определенный знак.
Задача 3. Найдите все значения a, при которых неравенство (a + 4)x2 + 2ax + 3a – 6 > 0 выполняется для всех значений x.
Решение. 1) Пусть a = – 4, тогда линейное неравенство 8x – 18 > 0 выполнено не для всех значений x, а только для x > 9.
2) Пусть a < – 4, тогда график
y = (a + 4)x2 + 2ax + 3a – 6
– парабола, ветви которой направлены вниз. Множество значений такой функции не ограничено снизу, поэтому неравенство (a + 4)x2 + 2ax + 3a – 6 > 0 перестает быть справедливым для достаточно больших x. Следовательно, при a < – 4 задача решений не имеет.
3) Пусть a > – 4, тогда график
y = (a + 4)x2 + 2ax + 3a – 6
– парабола, ветви которой направлены
вверх. В этом случае неравенство (a + 4)x2 + 2ax +
3a – 6 > 0 справедливо при всех x, если отрицателен
дискриминант уравнения (a + 4)x2 + 2ax + 3a – 6 = 0.
Решением этого неравенства является множество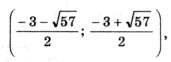 
,
что с учетом условия a > – 4 даст нам нужный
Ответ.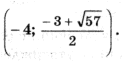
Необходимым и достаточным условием того, что квадратное уравнение имеет действительные корни, является неотрицательность дискриминанта. Вместе с тем, можно придумать много других достаточных (но не необходимых!) условий существования действительных корней квадратного трехчлена, подобных тому, которое доказано в следующей задаче.
Задача 4.
Доказать, что если для коэффициентов квадратного уравнения ax2 + bx + c = 0 выполнено неравенство ax2 + bx + c < 0, то уравнение имеет действительные корни.
Решение. Обозначим левую часть уравнения f(x), т. е.
f(x) = ax2 + bx + c.
Заметим, что f(0) = с, а f(1) = a + b + с, тогда неравенство из условия задачи можно переписать в виде
f(1)•f(0) < 0.
Поскольку f(x) непрерывна, а f(0) и f(1) – разного знака, то f(x) принимает значение ноль в некоторой точке x интервала (0; 1), то есть f(x) = 0. Таким образом, x = x – действительный корень исходного уравнения.
Составить квадратное уравнение по двум известным его корням – задача несложная. Оказывается, чтобы составить квадратное уравнение с рациональными коэффициентами, иногда (но не всегда) достаточно знать только один его корень.
Задача 5. Составить квадратное уравнение с
рациональными коэффициентами, один из корней
которого равен .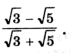
Решение. Преобразуем
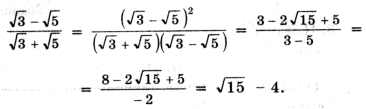
Пусть x2 + px + q = 0 (где p и q –
рациональные числа) – искомое уравнение.
Поскольку число 
– его корень, то
По условию p и q – рациональные, поэтому
число
(31 + q – 4p) – рациональное, а следовательно,
рациональным должно быть и число 
что возможно лишь в случае p = 8. Но тогда из соотношения (*) следует, что и (31 + q – 4p) = 0.
Итак, получили систему
Таким образом, искомое уравнение – это x2 + 8x + 1 = 0. Заметим, что, умножая все коэффициенты этого уравнения на любое отличное от нуля рациональное число, тоже получим уравнение, являющееся ответом к задаче.
Ответ: например, x2 + 8x + 1 = 0.
Заметим, что для квадратного уравнения с
рациональными коэффициентами справедливо
утверждение: если число вида 
является его
корнем,то сопряженное данному число 
– тоже является того же уравнения. А зная два
числа, легко составить квадратное уравнение,
корнями которого они являются.
При решении некоторых задач оказывается полезным помнить формулу, по которой находятся координаты вершины параболы – графика квадратичной функции.
Задача 6. При каких значениях p вершина параболы y = x2 + 2px + 13 лежит на расстоянии 5 от начала координат?
Решение. Абсцисса вершины параболы y = ax2
+ bx + c находится по формуле 
а ордината как
y0 = ax02 + bx0 + c.
В нашем случае
y0 = (– p)2 + 2p(– p) + 13 = p2 – 2p2 + 13 = 13 – p2.
Расстояние от вершины параболы (x0; y0) до начала координат находим по формуле
откуда
p2 = (13 – p2)2 = 25 Ы p4 = 25p2 + 144 = 0.
Решая полученное биквадратное уравнение заменой t = p2, находим
Ответ: {± 3; ± 4}.
Задача 7. Найти все значения y, при которых квадратное уравнение (y + 2)x2 – 2yx – y = 0 имеет два корня, расположенные на числовой прямой симметрично относительно точки x = 1.
Решение. Прежде всего заметим, что y № – 2, иначе уравнение не будет квадратным. Далее, уравнение имеет корни, если
Ось симметрии параболы проходит через ее вершину, поэтому корни данного квадратного уравнения расположены симметрично относительно точки x = 1 в том случае, если x0 = 1 – абсцисса вершины параболы, то есть
Это уравнение равносильно y = y + 2 (при условии y № – 2, не имеющему решений.
Ответ: y О Ж.
Вероятно, Вы заметили, что среди разобранных нами заданий не было задач на применение теоремы Виета. Этой теме будет посвящена целиком наша следующая публикация.
Задачи для самостоятельного решения
1–2. Для каждого значения параметра a:
1. Решите уравнение (a + 1)x2 + (a + 1)x + a – 2 = 0.
2. Решите неравенство .
3. При каких значениях m неравенство
(m + 1)x2 – (m – 1)x + 3m – 3 < 0
справедливо при всех x О R?
4. О квадратном трехчлене f(x) = x2 + px + q известно, что f(1) = 3 и f(3) < 1. Какие значения может принимать f(– 1)?
5. При каких значениях m трехчлен
y = (6m – 5)x2 – 5(m – 1)x + 2m – 6
есть полный квадрат?
6. Докажите, что уравнение
(x – 1)(x + 3) + m(x – 2)(x – 4) = 0
имеет корни при любом m О R.
7. Найдите все значения a, при которых квадратное уравнение ax2 + 2(a + 1)x + a + 3 = 0 имеет два различных корня.
8. Составить приведенное квадратное уравнение с рациональными коэффициентами, если один из его корней равен .
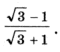
9. Составьте уравнение касательной к параболе y = 2x2 + 8x, перпендикулярной оси ординат.
10. При каких значениях a графики функций y = 2ax + 1 и y = (a – 6)x2 – 2 не пересекаются?
11. При каких значениях a функция f(x) = – x2 + (a – 1)x + 2 монотонно возрастает на интервале (1; 2)?
Ответы
1. 
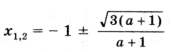при a > – 1; нет решений при a Ј – 1.
2. 
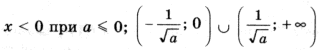при a > 0.
3. m < 2.
4. f(– 1) > 13. 5. m = 5. 6. Указание: найдите два значения x, при которых левая часть уравнения принимает значения разных знаков, а затем воспользуйтесь непрерывностью квадратичной функции.
7. a О (– Ґ; 0) И (0; 1). 8. x2 – 4x + 1 = 0. 9. y = – 8. 10. a О (–– 6; 3). 11. a О [–5; + Ґ).
Список использованной литературы
Васильева В.А., Кудрина Т.Д., Молодожникова Р.Н. Методическое пособие для поступающих в вузы. – М.: Изд-во МАИ, 1992.
РодионовЕ.М. Справочник по математике для поступающих в вузы: Решение задач с параметрами. – М.: МЦ «Аспект», 1992.
Табачников С.Л. Многочлены: Методические разработки для учащихся ОЛ «ВЗМШ» Российской академии образования при МГУ. – М.: Фазис, 1996.
Н. Антонова, С.
Солодовников,
Москва
