Комплексные числа

1. Понятие мнимой единицы

Допустим, что существует такое число, квадрат которого равен – 1. Обозначим это число буквой i; тогда можно записать: i² = – 1.

Число i будем называть мнимой единицей (i – начальная буква французского слова imaginaire – «мнимый»), а предыдущее равенство будем считать определением мнимой единицы.

Из этого равенства находим

Введение мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.

Например,

 2. Степени мнимой единицы

Рассмотрим степени мнимой единицы:

i;
i² = – 1;
i³ = i²Чi = (– 1)i = – i;
i⁴ = i³Чi = – iЧi = – i² = – (– 1) = 1;
i⁵ = i⁴Чi = 1Чi = i;
i⁶ = i⁵Чi = iЧi = i² = – 1;
i⁷ = i⁶Чi = (– 1)Чi = – i;
i⁸ = i⁷Чi = – iЧi = 1;
. . . . . . . . . . . . . . . . . . . . . . . . . .

Если выписать все значения степеней числа i, то мы получим такую последовательность: i, – 1, – i, 1, i, – 1, – i, 1 и т. д. Легко видеть, что значения степеней числа i повторяются с периодом, равным 4.

Так, i = i, i² = – 1, i³ = – i, i⁴ = 1, i⁵ = i, i⁶ = – 1, i⁷ = – i, i⁸ = 1, i⁹ = i, i¹⁰ = – 1, i¹¹ = – i, i¹² = 1.

Таким образом, если показатель степени числа i делится на 4, то значение степени равно 1; если при делении показателя степени на 4 в остатке получается 1, то значение степени равно i; если при делении показателя степени на 4 получается остаток 2, то значение степени равно – 1; наконец, если при делении на 4 остаток равен 3, то значение степени равно – i. Пользуясь этим, можно вычислять любую степень числа i.

Пример 1. Найти: i²⁸; i³³; i¹³⁵.

Решение. Имеем 28 = 4Ч7 (нет остатка); 33 = 4Ч8 + 1; 135 = 4Ч33 + 3.

Соответственно получим i²⁸ = 1; i³³ = i; i¹³⁵ = – i.

1–7. Вычислите:

1. i⁶⁶; i¹⁴³; i²¹⁶; i¹³⁷.
2. i⁴³ + i⁴⁸ + i⁴⁴ + i⁴⁵.
3. (i³⁶ + i¹⁷)i²³.
4. (i¹³³ + i¹¹⁵ + i²⁰⁰ + i¹⁴²)(i¹⁷ + i³⁶).
5. i¹⁴⁵ + i¹⁴⁷ + i²⁶⁴ + i³⁴⁵ + i¹¹⁷.
6. (i¹³ + i¹⁴ + i¹⁵)i³².
7. (i⁶⁴ + i¹⁷ + i¹³ + i⁸²)(i⁷² – i³⁴).

3. Определение комплексного числа

Мы знакомы с действительными числами и с мнимыми единицами. Рассмотрим теперь числа нового вида.

Определение 1. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, будем называть комплексными.

Число a будем назвать действительной частью комплексного числа, bi – мнимой частью комплексного числа, b – коэффициентом при мнимой части. Возможны случаи, когда действительные числа a и b могут быть равными нулю. Если a = 0, то комплексное число bi называется чисто мнимым. Если b = 0, то комплексное число a + bi равно a и называется действительным. Если a = 0 и b = 0 одновременно, то комплексное число 0 + 0i равно нулю. Итак, мы получили, что действительные числа и чисто мнимые числа представляют собой частные случаи комплексного числа.

Запись комплексного числа в виде a + bi называется алгебраической формой комплексного числа.

Два комплексных числа a + bi и c + di условились считать равными тогда и только тогда, когда в отдельности равны их действительные части и коэффициенты при мнимой единице, т. е. a + bi = c + di, если a = c и b = d.

Пример 2. Найти x и y из равенства:

а) 3y + 5xi = 15 – 7i;
б) (2x + 3y) + (x – y)i = 7 + 6i.

Решение. а) Согласно условию равенства комплексных чисел имеем 3y = 15, 5x = – 7. Отсюда

б) Из условия равенства комплексных чисел следует

Умножив второе уравнение на 3 и сложив результат с первым уравнением, имеем 5x = 25, т. е. x = 5. Подставим это значение во второе уравнение: 5 – y = 6, откуда y = – 1. Итак, получаем ответ: x = 5, y = – 1.

8–13. Найдите значения x и y из равенств:

8. 7x + 5i = 1 – 10iy.
9. (2x + y) – i = 5 + (y – x)i.
10. x + (3x – y)i = 2 – i.
11. (1 + 2i)x + (3 – 5i)y = 1 – 3i.
12. (2 – i)x + (1 + i)y = 5 – i.
13. (3i – 1)x + (2 – 3i)y = 2 – 3i.

4. Действия над комплексными числами в алгебраической форме

Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.

Пример 3. Даны комплексные числа z₁ = 2 + 3i, z₂ = 5 – 7i. Найти:

а) z₁ + z₂;    б) z₁ – z₂;    в) z₁z₂.

Решение.

а) z₁ + z₂ = (2 + 3i) + (5 – 7i) = 2 + 3i + 5 – 7i = (2 + 5) + (3i – 7i) = 7 – 4i;
б) z₁ – z₂ = (2 + 3i) – (5 – 7i) = 2 + 3i – 5 + 7i = (2 – 5) + (3i + 7i) = – 3 + 10i;
в) z₁z₂ = (2 + 3i)(5 – 7i) = 10 – 17i + 15i – 21i² =  10 – 14i + 15i + 21 = (10 + 21) + (– 14i + 15i) = 31 + i
(здесь учтено, что i² = – 1).

14–21. Произведите сложение и вычитание комплексных чисел:

14. (3 + 5i) + (7 – 2i).
15. (6 + 2i) + (5 + 3i).
16. (– 2 + 3i) + (7 – 2i).
17. (5 – 4i) + (6 + 2i).
18. (3 – 2i) + (5 + i).
19. (4 + 2i) + (– 3 + 2i).
20. (– 5 + 2i) + (5 + 2i).
21. (– 3 – 5i) + (7 – 2i).

22–29. Произведите умножение комплексных чисел:

22. (2 + 3i)(5 – 7i).
23. (6 + 4i)(5 + 2i).
24. (3 – 2i)(7 – i).
25. (– 2 + 3i)(3 + 5i).
26. (1 –i)(1 + i).
27. (3 + 2i)(1 + i).
28. (6 + 4i)Ч3i.
29. (2 – 3i)(– 5i).

Замечание. При выполнении умножения можно использовать формулы:

(a± b)² = a² ± 2ab + b²,
(a ± b)³ = a³ ± 3a²b + 3ab ± b³.

Пример 4. Выполнить действия:

а) (2 + 3i)²;    б) (3 – 5i)²;    в) (5 + 3i)³.

Решение.

а) (2 + 3i)² = 4 + 2Ч2Ч3i + 9i² = 4 + 12i – 9 = – 5 + 12i;
б) (3 – 5i)² = 9 – 2Ч3Ч5i + 25i² = 9 – 30i – 25 = – 16 – 30i;
в) (5 + 3i)³ = 125 + 3Ч25Ч3i + 3Ч5Ч9i² + 27i³;
так как i² = – 1, а i³ = – i, то получим (5 + 3i)³ = 125 + 225i – 135 – – 27i = – 10 + 198i.

30–37. Выполните действия:

30. (3 + 5i)².
31. (2 – 7i)².
32. (6 + i)².
33. (1 – 5i)².
34. (3 + 2i)³.
35. (3 – 2i)³.
36. (4 + 2i)³.
37. (5 – i)³.

Рассмотрим теперь применение формулы

(a + b)(a – b) = a² – b².     (*)

Пример 5. Выполнить действия:

а) (5 + 3i)(5 – 3i);   
б) (2 + 5i)(2 – 5i);
в) (1 + i)(1 – i).

Решение.

а) (5 + 3i)(5 – 3i) = 5² – (3i)² = 25 – 9i² = 25 + 9 = 34;
б) (2 + 5i)(2 – 5i) = 2² – (5i)² = 4 + 25 = 29;
в) (1 + i)(1 – i) = 1² – i² = 1 + 1 = 2.

38–43. Выполните действия:

38. (3 + 2i)(3 – 2i).
39. (5 + i)(5 – i).
40. (1 – 3i)(1 + 3i).
41. (7 – 6i)(7 + 6i).
42. (a + bi)(a – bi).
43. (m – ni)(m + ni).

Обратим внимание на то, что при использовании формулы (*) всегда получается частный случай комплексного числа – действительное число, а комплексные числа, которые мы умножаем, являются сопряженными.

Определение 2. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.

Мы видим, что произведение двух сопряженных чисел всегда равно действительному числу. Воспользуемся этим свойством для выполнения деления двух комплексных чисел. Чтобы выполнить деление, произведем дополнительное действие: умножим делимое и делитель на комплексное число, сопряженное делителю.

Пример 6. Выполнить деление:

Решение.

а) Имеем

Произведем умножение для делимого и делителя в отдельности:

(2 + 3i)(5 + 7i) = 10 + 14i + 15i + 21i² = – 11 + 29i;
(5 – 7i)(5 + 7i) = 25 – 49i² = 25 + 49 = 74.

Итак,

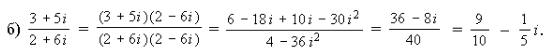
44–55. Выполните деление:

56–60. Выполните действия:

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.

Пример 7. Решите уравнение:

а) x² – 6x + 13 = 0;    б) 9x² + 12x + 29 = 0.

Решение. а) Найдем дискриминант по формуле

D = b² – 4ac.

Так как a = 1, b = – 6, c = 13, то

D = (– 6)2 – 4Ч1Ч13 = 36 – 52 = – 16;

Корни уравнения находим по формулам

б) Здесь a = 9, b = 12, c = 29. Следовательно,

D = b² – 4ac =12² – 4Ч9Ч29 = 144 – 1044 = – 900,

Находим корни уравнения:

Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.

62–65. Решите уравнения:

62. x² – 4x + 13 = 0.
63. x² + 3x + 4 = 0.
64. 2,5x² + x + 1 = 0.
65. 4x² – 20x + 26 = 0.

5. Геометрическая интерпретация комплексного числа

Комплексное число z = a + bi можно изобразить точкой Z плоскости с координатами (a; b) (рис. 1). Для этого выберем на плоскости декартову прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которую называют действительной (или вещественной) осью; чисто мнимые числа – точками оси ординат, которую будем называть мнимой осью.

Каждой точке плоскости с координатами (a; b) соответствует один и только один вектор с началом O(0; 0) и концом Z(a; b). Поэтому комплексное число z = a + bi можно изобразить в виде вектора с началом в точке O(0; 0) и концом в точке Z(a; b).

Пример 8. Изобразить на плоскости числа z₁ = 5; z₂ = – 3i; z₃ = 3 + 2i; z₄ = 5 – 2i; z₅ = – 3 + 2i; z₆ = – 1 – 5i.

Решение. Заданные числа изображены на рис. 2.

Определение 4. Аргументом комплексного числа называется угол j, который образует вектор с положительным направлением оси абсцисс. Величину угла j можно найти с помощью формул: 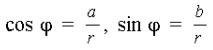               (2)

Эта система имеет бесчисленное множество решений вида j + 2 pk, где k – любое целое число. Таким образом, любое комплексное число z имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 2p. Если k = 0, то мы получим главное значение аргумента j, которое и будем называть аргументом комплексного числа.

Из соотношений и

следует  a = r cos j, b = r sin j.

Если в запись комплексного числа z вместо a и b подставить эти значения, то получим

z = a + bi = r cos j + ir sin j = r (cos j + i sin j).

Таким образом, мы получили новую форму записи комплексного числа:

z = r (cos j + i sin j), (3)

которая называется тригонометрической формой комплексного числа.

Сформулируем правило перехода от алгебраической формы комплексного числа к тригонометрической.

1. Находят модуль комплексного числа r, для чего используют формулу

2. Для нахождения j сначала определяют геометрически, в какой четверти находится точка z.

3. Составляют уравнения и и по решению одного из них находят угол j.

4. Записывают комплексное число z в тригонометрической форме.

Пример 9. Записать в тригонометрической форме комплексное число z = 1 + i.

Решение.

1) Так как a = 1, b = 1, то

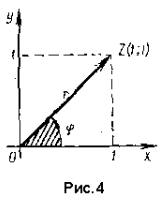2) Изобразим число z геометрически (рис. 4). Мы видим, что числу z соответствует точка Z, лежащая в I четверти, и вектор z.

3) Составим соотношения и т. е.

Этим соотношениям соответствует в I четверти угол

4) Так как

то тригонометрическая форма заданного комплексного числа имеет вид

Пример 10. Записать число в тригонометрической форме.

Решение. 1) Здесь

Следовательно,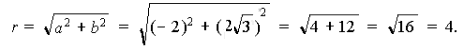

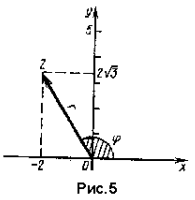2) Изобразим число z геометрически (рис. 5). Мы видим, что числу z соответствует точка Z, лежащая во II четверти, и вектор z.

 3) Находим

Этим соотношениям соответствует угол j = 180° – 60° = 120°  .

4) Запишем заданное число в тригонометрической форме:

Пример 11. Записать в тригонометрической форме чисто мнимое число z = – 3i.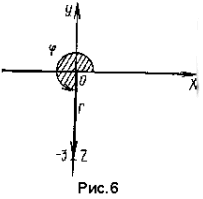

Решение. 1) Запишем данное число в виде z = 0 – 3i. Значит, a = 0, b = – 3, откуда

2) Точка, соответствующая геометрически числу z = – 3i, лежит на мнимой оси (рис. 6).

3) Аргумент этого числа равен ,

так как угол отсчитывается от положительного направления оси Ox против часовой стрелки.

4) Запишем данное число в тригонометрической форме:

66–71. Запишите в тригонометрической форме комплексные числа:

7. Показательная форма комплексного числа

Если комплексному числу z = (cos j + i sin j), модуль которого равен 1, поставить в соответствие показательное выражение eⁱj, то получим соотношение

cos j + i sin j = eⁱj, (4)

которое называется формулой Эйлера.

Любое комплексное число z можно записать в виде z = reⁱj.

Эта форма записи комплексного числа называется показательной формой.

Итак, существуют три формы записи комплексного числа:

z = a + bi – алгебраическая форма;
z = r (cos j + i sin j) – тригонометрическая форма;
z = reⁱj – показательная форма.

Пример 12. Записать число

в показательной форме.

Решение. Здесь

Следовательно, показательная форма числа имеет вид

Продолжение следует