Согласно распоряжению Московского городского департамента по образованию в 1999 году в 9-х классах общеобразовательных средних школ города Москвы будет проведен обязательный устный экзамен по планиметрии.
В 1999 году в издательстве «Дрофа» издан сборник билетов, рекомендованный Министерством общего и профессионального образования РФ для использования при проведении устных экзаменов в 9-х классах общеобразовательных школ, содержащий, в частности, билеты по планиметрии. Особенностью этих билетов является то, что их структура не привязана к конкретному школьному учебнику, а полностью опирается только на федеральную программу по геометрии.
В настоящей статье предлагаются методические рекомендации по организации повторения планиметрии в 9-х классах. Эти рекомендации разработаны таким образом, чтобы их можно было использовать во всех девятых классах независимо от учебника, по которому велось обучение. Мы предполагаем, что их можно применять как для закрепления изученного материала, так и при подготовке к экзаменам по планиметрии в соответствии с билетами, рекомендованными Министерством образования. В точном соответствии с предлагаемой методикой издательство «Генжер» подготовило рабочую тетрадь «Повторение курса планиметрии».
Заключительное повторение курса планиметрии проводится с целью систематизировать ранее полученные учащимися знания и приобретенные ими умения и навыки. Из федеральной программы по геометрии следует:
· цели и задачи обучения планиметрии определяются как систематическое изучение свойств основных геометрических фигур на плоскости, развития логического мышления, пространственных представлений и геометрической интуиции и подготовке геометрического аппарата для изучения смежных дисциплин и курса стереометрии;
· уровень и объем умений и навыков, обязательных для овладения учащимися в процессе изучения курса планиметрии, характеризуется рациональным сочетанием логической строгости и геометрической наглядности, направленностью геометрического аппарата на вычисления, доказательства и построения;
· основная содержательная
линия курса планиметрии определяется как
учение о свойствах геометрических фигур (точки,
прямые, углы, треугольники, четырехугольники,
многоугольники, окружность и круг
и т. д.).
Из сказанного выше можно
заключить, что систематизацию знаний и умений
учащихся по курсу планиметрии удобно построить
на основе систематизации свойств основных
геометрических фигур, а именно, треугольников,
четырехугольников, многоугольников, окружности
и круга. Таким образом, весь учебный материал
курса организуется по принципу наиболее полного
описания свойств и признаков геометрических
фигур.
Повторение целесообразно провести в 3 этапа.
Первый этап. Учебный материал группируется вокруг треугольника. Он является одной из основных фигур планиметрии. Повторение теорем, отражающих свойства и признаки различных треугольников, позволяет систематизировать умения логического поиска доказательных рассуждений, т. е. умения при доказательстве теорем исследовать, что требуется для доказательства.
Второй этап. Учебный материал группируется вокруг многоугольников, включая и четырехугольники, где содержание геометрических задач обогащается разнообразием геометрических ситуаций.
Особенности второго этапа:
– умение производить поиск логической обоснованности или логической закономерности различных свойств геометрических фигур у учащихся находятся в лучшем состоянии, чем на первом этапе. Поэтому формально-логический аспект повторения отходит на второй план. Логические цепочки при доказательных рассуждениях заканчиваются на теоремах, повторение и систематизация которых была проведена на первом этапе. Умение же вычленить более сложные (по сравнению с первым этапом) геометрические конфигурации выступает на первое место;
– возможность и неизбежность повторения во второй раз различных свойств треугольников.
Третий этап. Повторение свойств окружности (круга) и ее элементов, т. е. нелинейной планиметрии. Такое повторение должно сочетать в себе как поиск свернутых доказательных рассуждений, так и сведение более сложных геометрических построений к более простым. Этот этап подытоживает все богатство методов и приемов решения геометрических задач, демонстрирует эффективность совместного использования всех методов.
Предлагаемый способ систематизации и анализ различных учебных пособий по геометрии позволяет:
– выделить в каждом учебнике, реализующем федеральную программу, инвариативную (основную) часть, реализующую программу курса планиметрии; вариативную часть, учитывающую особенности построения различных курсов планиметрии (специфические особенности того или иного учебного пособия при этом должны учитываться в той мере, которая позволяет выполнить основные программные требования);
– провести группировку повторяемого материала вокруг указанных выше трех групп основных геометрических фигур.
Таким образом, курс повторяется в три этапа, и на каждом этапе происходит сочетание повторения учебного материала с некоторыми моментами повторения и закрепления навыков поиска доказательных рассуждений и решения содержательных задач. Характерной чертой предложенного приема организации повторения является то обстоятельство, что учащимся предлагается многократно возвращаться к ранее пройденному материалу, вспомнить его.
Отбор инвариативной части содержания был проведен с соответствии с требованиями действующей программы, отбор же дополнительного учебного материала варьируется в зависимости от способа изложения курса планиметрии в конкретном учебнике.
Содержание повторения
Инвариативная часть
Первый этап
1. Определение треугольника
и его элементов: угла, стороны, высоты, медианы и
биссектрисы треугольника.
2. Понятие о равных треугольниках.
3. Признаки равенства треугольников. Признаки
равенства прямоугольных треугольников.
4. Свойство углов при основании
равнобедренного треугольника. Признак
равнобедренного треугольника. Свойство медианы
равнобедренного треугольника, проведенной к
основанию.
5. Сумма углов треугольников. Внешний угол
треугольника и его свойства.
6. Признак равенства прямоугольных
треугольников.
7. Средняя линия треугольника. Теорема Фалеса.
8. Теорема Пифагора. Следствия из теоремы
Пифагора. Решение прямоугольных треугольников.
9. Признаки подобия треугольников.
10. Решение и построение треугольников.
Теорема синусов. Теорема косинусов. Неравенство
треугольника. Векторы.
11. Площадь треугольника.
Учебный материал этого этапа относится, в основном, к началу изучения курса планиметрии. Отсюда вытекает необходимость напомнить учащимся некоторые логические рассуждения. Например, схему доказательства от противного, структуру прямого и обратного утверждения, что такое свойство фигуры и что такое признак. С другой стороны, треугольник является наиболее употребительной фигурой в планиметрии, и основные факты: определения, формулировки теорем, формулы для вычисления элементов треугольника, хорошо известны учащимся. Исходя из этого, можно за основную форму организации повторения на первом этапе принять обзорные лекции, в которых кратко осветить весь теоретический материал, обращая внимание учащихся, как на логику доказательств, так и на их поиск. Лекции иллюстрируются и дополняются решением задач, которые либо включаются в содержание лекций и демонстрируются учителем, либо решаются учащимися самостоятельно на специально выделенных уроках. Деятельность ученика при этом заключается в составлении конспекта лекций.
Второй этап
1. Определение
параллелограмма. Признаки и свойства
параллелограмма. Определение прямоугольника.
Свойство диагоналей прямоугольника. Определение
ромба. Свойство диагоналей ромба. Квадрат.
Трапеция, средняя линия трапеции.
2. Многоугольники. Выпуклые многоугольники.
Сумма углов выпуклого многоугольника. Внешний
угол многоугольника. Правильные многоугольники.
3. Площадь прямоугольника, параллелограмма,
трапеции, многоугольников.
Так как материал второго этапа повторения, в основном, использует свойства треугольника, повторение которых прошло на первом этапе, и элементы доказательств теорем первого этапа, то рекомендуется проведение уроков в виде бесед, в ходе которых учащиеся под руководством учителя доказывают основные теоремы и решают задачи.
Третий этап
1. Определение окружности и
ее элементов: центра, радиуса, хорды, касательной
к окружности.
2. Теорема о центре окружности, вписанной в
треугольник. Теорема о центре окружности,
описанной около треугольника.
3. Углы, вписанные в окружность. Центральный
угол и его мера.
4. Окружность, вписанная и описанная около
правильного многоугольника. Формулы, выражающие
соотношения между стороной правильного
многоугольника и радиусом вписанной (описанной)
окружности.
5. Длина дуги окружности.
6. Круг. Площадь круга. Площадь кругового
сектора. Площадь кругового сегмента.
Поскольку все основные методы планиметрии к началу третьего этапа повторения учащимися проанализированы в различных аспектах применения, то рекомендуется повторение содержания этого этапа провести в процессе самостоятельной работы учащихся: составить конспекты теоретического материала по плану, предложенному учителем, и решить рекомендованные задачи. Фактически третий этап повторения является контрольным. Здесь проверяются и дорабатываются умения и навыки учащихся проводить доказательные рассуждения и применять весь багаж знаний по планиметрии в ходе решения содержательных задач. На этом этапе учитель выступает в роли консультанта и проводит индивидуальную работу с учащимися.
Примерное планирование заключительного повторения
(16 часов)
Первый этап (7 ч)
Лекции по теме «Треугольники» 3 ч
Практические занятия по теме лекций 3 ч
Решение и построение треугольников (лекция или беседа) 1 ч
Второй этап (3 ч)
Беседы по теме «Многоугольники» 2 ч
Решение задач 1 ч
Третий этап (2 ч)
Самостоятельные работы по теме «Окружность» 2 ч
Решение задач (4 ч)
Методические рекомендации к проведению заключительного повторения
Первый этап. Тема «треугольники»
Учитывая подготовку класса, его особенности при проведении первого этапа повторения, учитель должен предусмотреть некоторые варианты. Например, можно всю тему «Решение треугольников» перенести на упражнения или самостоятельную работу. После любой из лекций учитель может провести два часа решения задач, если сочтет это необходимым, сократив тем самым число часов на решение задач в конце заключительного повторения. Если учитель сочтет целесообразным прочитать все лекции подряд, то из указанных к ним типов задач можно сформировать домашние задания.
В процессе чтения лекций доказываются только основополагающие и наиболее сложные в логическом построении теоремы. Во всех остальных случаях, как правило, внимание фиксируется на наиболее важных моментах доказательств.
Как при проведении доказательных рассуждений, так и в процессе поиска решения задач следует обращать внимание учащихся на геометрические конфигурации, вычленяемые из чертежа, иллюстрирующего условие задачи, которые позволяют создать наглядную основу, обеспечивающую эвристический переход от содержания задачи к ранее установленным геометрическим фактам.
Лекция 1
1. Дать определения
треугольника и равных треугольников,
сформулировать все аксиомы и теоремы,
используемые в доказательствах признаков
равенства и записать их на доске.
2. Определить равенство треугольников и
провести доказательство трех признаков
равенства.
3. Сформулировать две теоремы, которые
являются примерами прямой и обратной теорем:
В равнобедренном треугольнике углы при основании равны.
Если в треугольнике два угла равны, то он равнобедренный.
Доказательство прямой теоремы опирается на первый признак равенства треугольников, а обратной – на второй признак. В качестве примеров прямой и обратной теорем можно предложить учащимся следующее задание:
Докажите, что у равностороннего треугольника все углы равны.
Сформулируйте и докажите теорему, обратную утверждению предыдущей задачи.
4. После повторения с учащимися определения высоты, медианы и биссектрисы треугольника напомнить теорему о медиане равнобедренного треугольника. Ее доказательство опирается на определение медианы, что позволяет выделить недостающий элемент для применения первого признака равенства треугольников. При доказательстве утверждения «Медиана... есть высота» выделяется базовая геометрическая конфигурация – смежные углы.
5. Для закрепления материала лекции полезно рассмотреть признаки равенства специфических треугольников (равнобедренных, прямоугольных, равносторонних), т. е. выяснить вопрос – как изменяются признаки равенства треугольников, если треугольник (по определению) обладает определенными свойствами. В зависимости от уровня подготовки класса эти признаки можно попытаться сформулировать с помощью учащихся или дать в виде задач. Признаки равенства прямоугольных треугольников учащиеся знают из курса планиметрии, а для равнобедренных и равностороннего треугольников их полезно сформулировать:
Докажите равенство равнобедренных треугольников по:
а) боковой стороне и углу при вершине;
б) основанию и углу при основании;
в) основанию и боковой стороне.
6. Следствием из равенства треугольников является утверждение, что у равных треугольников все соответствующие элементы равны, а именно: соответствующие медианы, биссектрисы, высоты, средние линии, радиусы вписанных и описанных окружностей. Для этого можно предложить задачи типа:
Докажите, что у равных треугольников ABC и A1B1C1 медианы, проведенные к соответственно равным сторонам, равны.
Биссектрисы, проведенные из вершин A и A1, равны.
Во всех этих задачах на основе свойств медианы, высоты, средней линии, радиуса, проведенного в точку касания, следует выделить пару равных треугольников.
7. Рассматривая свойства равнобедренного треугольника, можно еще раз подчеркнуть, что высота, проведенная к основанию, является медианой и биссектрисой, а биссектриса угла при вершине – медианой и высотой. При этом полезно решить задачи:
Докажите, что если в треугольнике высота делит основание пополам, то треугольник равнобедренный.
Докажите, что если в треугольнике медиана перпендикулярна стороне, к которой она проведена, то треугольник равнобедренный.
Докажите, что в равностороннем треугольнике все медианы, высоты и биссектрисы равны.
8. Для индивидуальной работы по карточкам можно предложить более сложные задачи:
На прямой, пересекающей стороны угла, найдите точку, равноудаленную от сторон этого угла.
Через точку, данную внутри или вне угла, проведите такую прямую, которая отсекала бы на сторонах угла равные отрезки.
Постройте прямую, перпендикулярную отрезку AB в точке B, при условии, что отрезок нельзя продлить за точку B.
Лекция 2
1. Ввести определения параллельности прямых и углов, образованных двумя прямыми, пересеченными третьей. Затем сформулировать аксиому о параллельных прямых, при этом обратить внимание учащихся на существование «не более одной прямой, параллельной данной». Сформулировать признаки параллельности прямых и свойства углов при параллельных прямых и секущей.
Теорема «Если внутренние накрест лежащие углы равны, то прямые параллельны» доказывается методом от противного.
Этот метод широко применяется как при доказательстве теорем, так и при решении задач. При его использовании выполняется следующая последовательность логических шагов:
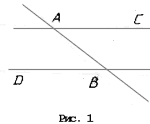
Дано: РCAB = Р ABD.
Доказать: AC || DB (рис. 1).
Предположим, что AС![]() DC. Что это
значит? Это значит, что данные теоремы
дополняются еще одним условием, т. е. данные
можно записать в виде:
DC. Что это
значит? Это значит, что данные теоремы
дополняются еще одним условием, т. е. данные
можно записать в виде:
Дано: РCAB = РABD, AC![]() DC.
DC.
При доказательстве теоремы «Если внутренние накрест лежащие углы равны, то прямые параллельны» приходим к противоречию со свойствами принадлежности точек и прямых на плоскости.
2. Доказать теорему о сумме углов треугольника и сформулировать следствия из нее, доказать теорему о внешнем угле треугольника.
3. Для закрепления материала лекции, связанного с признаками и свойствами параллельных прямых, рекомендуются задачи:
Докажите, что два перпендикуляра к одной прямой параллельны.
При каком положении секущей все углы, образованные ею с двумя параллельными прямыми, равны?
Две параллельные прямые пересечены третьей прямой. При этом один из внутренних углов равен 140°. Под каким углом его биссектриса пересекает другую параллельную прямую?
4. Учащимся известны пары равных углов (вертикальные, накрест лежащие при параллельных прямых, вписанные углы, опирающиеся на одну дугу) и пары углов, в сумме составляющие 180° (смежные и односторонние при параллельных прямых).
Следует найти еще пары углов, равных или в сумме составляющих 180°.
Докажите, что если стороны одного угла соответственно параллельны (перпендикулярны) сторонам другого угла, то такие углы равны или их сумма равна 180°.
Докажите, что если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы равны или их сумма равна 180°.
5. Теорема о сумме углов треугольника дает возможность расширить знания учащихся о свойствах треугольников.
Докажите, что биссектрисы внутреннего и внешнего углов треугольника при одной вершине треугольника перпендикулярны.
Докажите, что прямая, проведенная через вершину равнобедренного треугольника параллельно основанию, является биссектрисой внешнего угла при этой вершине.
Один угол равнобедренного треугольника равен разности остальных. Найдите углы треугольника.
Докажите, что угол между прямыми, содержащими биссектрисы острых углов прямоугольного треугольника, есть величина постоянная.
Докажите, что если два внешних угла треугольника равны, то треугольник равнобедренный.
6. Используя известный факт, что если острый угол прямоугольного треугольника равен 30°, то противоположный ему катет равен 0.5 гипотенузы, можно решить с учащимися следующие задачи, которые позволят установить новые свойства прямоугольных треугольников:
Определите отношение между сторонами треугольника, если его углы относятся как 1 : 2 : 3.
Найдите углы прямоугольного треугольника, если угол между биссектрисой и высотой, проведенным из вершины прямого угла, равен 15°.
Один из острых углов прямоугольного треугольника равен 30°. Докажите, что один из отрезков, на которые делит гипотенузу высота, проведенная из вершины прямого угла, в три раза больше другого.
7. Теорема о сумме углов треугольника может быть использована при решении задач на построение.
Постройте с помощью циркуля и линейки угол, равный: а) 60°; б) 30°; в) 45°.
Постройте с помощью циркуля и линейки угол, равный: а) 75°; б) 105°; в) 135°.
Разделите с помощью циркуля и линейки на три равные части угол, равный: а) 45°; б) 90°; в) 135°.
Лекция 3
1. Дать определение средней
линии треугольника и сформулировать теорему
Фалеса. Сформулировать теорему о средней линии
треугольника. Для доказательства параллельности
средней линии стороне треугольника через
середину стороны треугольника проводится
прямая, параллельная другой стороне, и, используя
теорему Фалеса, доказывается, что эта прямая
содержит среднюю линию треугольника.
2. Сформулировать признаки подобия
треугольников и привести их доказательства.
3. Для актуализации знаний учащихся по теме
«Подобные треугольники» рекомендуются задачи:
Докажите, что прямая, параллельная какой-нибудь стороне треугольника, отсекает от него подобный треугольник.
Докажите, что в подобных треугольниках соответственные (сходственные) стороны пропорциональны соответственным (сходственным): а) высотам; б) биссектрисам; в) медианам; г) средним линиям; д) радиусам вписанных окружностей.
Докажите, что в прямоугольном треугольнике высота, опущенная на гипотенузу, делит его на два треугольника, подобные исходному и друг другу.
Сформулируйте и докажите признаки подобия для: а) прямоугольных; б) равнобедренных; в) равносторонних треугольников.
Докажите, что отрезок, соединяющий основания двух высот остроугольного треугольника, отсекает треугольник, подобный данному.
Если при решении задач к лекции 2 было разобрано с учащимися решение задач к пункту 4, то задача:
Докажите, что если стороны одного треугольника соответственно параллельны или соответственно перпендикулярны сторонам другого треугольника, то такие треугольники подобны не вызовет затруднений при ее решении.
Лекция 4 (беседа)
Этот урок лучше проводить в форме беседы и решения задач под руководством учителя.
1. Рассмотреть прямоугольный треугольник и дать определения синуса, косинуса и тангенса острого угла. Сформулировать теорему Пифагора, записать основные формулы для решения прямоугольного треугольника (табл. 1). Равенства в последнем столбце можно вывести из подобия прямоугольных треугольников.
Таблица 1
После повторения теоремы Пифагора и ее следствий можно доказать обратную теорему.
Дан треугольник со сторонами a, b и c. Докажите теорему, обратную теореме Пифагора: если a2 + b2 = c2, то треугольник прямоугольный с прямым углом, противолежащим стороне c.
2. Напомнить учащимся правило треугольника и параллелограмма для сложения векторов. Определить скалярное произведение и вспомнить алгоритм нахождения косинуса угла между векторами. Сформулировать теорему косинусов, записать формулу, выяснить с учащимися, какой знак должен быть перед удвоенным произведением сторон.
После повторения теоремы косинусов целесообразно решить задачу:
Дан треугольник со сторонами a, b и c. Докажите, что если a2 + b2 Ј c2, то угол, противолежащий стороне c, – острый. Если же a2 + b2 і c2, то угол, противолежащий стороне c, – тупой.
3. Сформулировать теорему синусов. Ее доказательство основывается на определении синуса острого угла в прямоугольном треугольнике.
4. Сформулировать неравенство треугольника и следствия из теоремы синусов. Решение треугольников проводится одновременно с построением, при этом полезно воспользоваться таблицами 2, 3.
1. Постройте треугольник по стороне и двум углам.
Возможны два случая:
1) углы являются прилежащими к стороне a.
2) один из углов является противолежащим стороне a.В первом случае проводим построение и утверждаем, что в силу второго признака равенства треугольников решение единственно. Зная величины стороны a и углов a и b, можно найти угол (g = 180° – a – b) и стороны треугольника по теореме синусов. Во втором случае применяем теорему о сумме углов треугольника и строим третий угол. Задача сводится к первому случаю.
Таблица 2
Таблица 3
2. Построить треугольник по двум сторонам и углу.
Так же, как и в первой задаче, возможны два случая:
1) угол лежит между двумя данными сторонами.
2) угол является противолежащим одной из данных сторон.
В первом случае проводим построение и утверждаем, что в силу первого признака равенства треугольников задача имеет единственное решение. Зная величины сторон a, b и угла b, можно найти третью сторону по теореме косинусов c2 = a2 + b2 – 2abcos a, а углы по теореме синусов с учетом ограничения, что против большой стороны лежит больший угол.
Во втором случае строим угол. На его стороне от вершины откладываем отрезок, равный одной из данных сторон треугольника. Из конца отрезка, не совпадающего с вершиной угла, проводим дугу до пересечения с другой стороной угла радиусом, равным другой стороне треугольника. При различных значениях величин сторон и угла может быть два решения, одно решение и ни одного решения. Если выполнено неравенство a і b, то решение единственно.
Если a Ј b, то возможны три случая.
3. Построить треугольник по трем сторонам.
Решение единственно по третьему признаку равенства треугольников. При решении треугольника используется теорема косинусов.
5. В процессе повторения этой темы необходимо через решения задач повторить тригонометрический материал и векторы. Как правило, эти задачи просты, их можно использовать для работы со слабыми учениками.
В прямоугольном треугольнике гипотенуза равна a, а один из острых углов a. Найдите второй острый угол и катеты.
В прямоугольном треугольнике катет равен a, а противолежащий ему угол a. Найдите второй острый угол, противолежащий ему катет и гипотенузу.
В прямоугольном треугольнике дана гипотенуза a и острый угол a. Найдите катеты, их проекции на гипотенузу и высоту, проведенную из вершины прямого угла.
Докажите, что векторыперпендикулярны или равны нулю.
Даны векторы
При каком значении m эти векторы перпендикулярны?Даны вершины треугольника A(1; 1), B(4; 1), C(4; 5). Найдите косинусы углов треугольника.
Найдите угол между векторами
6. После окончания повторения материала, связанного с конфигурацией треугольника, полезно обсудить с учащимися вопрос о трех замечательных точках треугольника.
Докажите, что в треугольнике биссектрисы пересекаются в одной точке.
Докажите, что в треугольнике медианы пересекаются в одной точке.
Докажите, что в треугольнике высоты пересекаются в одной точке.Здесь мы приведем решение последней задачи:
Через каждую вершину треугольника ABC проведем прямую, параллельную противоположной стороне. В полученном треугольнике A1B1C1 стороны будут перпендикулярны высотам исходного треугольника ABC. Так как BC = B1A = AC1 как противоположные стороны параллелограмма, то A – середина стороны B1C1. Аналогично доказывается, что B – середина стороны A1C1 и C – середина стороны A1B1. Таким образом, высоты AD, BE и CF треугольника ABC являются серединными перпендикулярами для треугольника A1B1C1.
7. При рассмотрении темы
«Площадь треугольников» следует записать все
известные учащимся формулы для вычисления
площади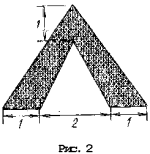 треугольника. При
этом полезно решить задачи по готовому чертежу.
треугольника. При
этом полезно решить задачи по готовому чертежу.
Найдите площадь заштрихованной фигуры, используя данные рисунка (рис. 2).
Кроме того, полезно обратить внимание учащихся на понятие «равновеликости площадей» через решение задач типа:
Разделите треугольник прямыми, проходящими через одну из его вершин на три части, площади которых относятся как 1 : 2 : 3.
Второй этап. Тема «многоугольники»
Как было сказано выше, второй этап повторения материала о многоугольниках организуется в форме беседы. Повторение теоретической части рассчитано на два урока. На первом уроке проводится беседа о свойствах четырехугольников: параллелограмма, прямоугольника, ромба, квадрата, трапеции. На втором уроке рассматривается материал о свойствах многоугольников. Теоретические вопросы при этом чередуются с решением задач, посвященных, как правило, доказательству дополнительных свойств рассматриваемых фигур. Доказательные рассуждения при этом следует строить, как правило, на основе идей и методов первого этапа повторения. Это позволяет еще раз повторить основные теоремы о треугольнике, и показать их роль в решении задач, в которых рассматриваются более сложные конфигурации.
1. Как правило, учащиеся легко выстраивают доказательства признаков и свойств четырехугольников. Поэтому при повторении важно подчеркнуть их родовые связи.
2. При повторении признаков и определений различных четырехугольников целесообразно в ходе решения задач найти новые признаки или применить известные в неожиданных ситуациях:
а) Для параллелограмма:
Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
б) Для прямоугольника:
В параллелограмме из вершин тупых углов на противолежащие стороны опущены перпендикуляры. Доказать, что полученный четырехугольник – прямоугольник.
Докажите, что если у параллелограмма все углы равны, то он – прямоугольник.
в) Для ромба:
Докажите, что четырехугольник, у которого все стороны равны, является ромбом.
После решения первой задачи данного пункта (2) и повторения признаков специальных четырехугольников интересно разобрать решение следующей задачи.
Середины сторон произвольного четырехугольника являются вершинами параллелограмма. Определите: вид данного четырехугольника, чтобы параллелограмм стал: а) прямоугольником; б) ромбом; в) квадратом.
3. Для систематизации и актуализации знаний учащихся о свойствах четырехугольников можно рекомендовать решить задачи:
а) Для параллелограмма:
Докажите, что в параллелограмме: а) сумма углов, прилежащих к одной стороне, равна 180°; б) сумма всех углов равна 360°.
Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии.
В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противоположного угла лежит на основании. Докажите, что периметр параллелограмма есть величина постоянная для данного треугольника.
б) Для ромба:
В ромбе одна из диагоналей равна стороне. Определите углы ромба.
Докажите, что диагонали ромба являются его осями симметрии.
В равносторонний треугольник вписан ромб так, что одна вершина у них общая, а три другие вершины ромба лежат на сторонах треугольника. Найдите: в каком отношении делят стороны треугольника вершины ромба.
в) Для квадрата:
Докажите, что прямые, проходящие через точку пересечения диагоналей квадрата параллельно его сторонам, являются осями симметрии квадрата.
Дан квадрат ABCD. На каждой его стороне отложены равные отрезки AA1 = BB1 = CC1 = DD1. Докажите, что четырехугольник A1B1С1D1 – квадрат.
г) Для трапеции:
Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен полуразности оснований.
Докажите, что если в трапеции диагонали являются биссектрисами углов при одном из оснований, то три стороны трапеции равны.
Докажите, что в равнобедренной трапеции:а) углы, прилежащие к одному основанию, равны;
б) диагонали равны;
в) треугольники, на которые диагонали делят трапецию, прилежащие к боковым сторонам, равны;
г) треугольники, на которые диагонали делят трапецию, прилежащие к основаниям, подобны. Нужно ли для доказательства этого положения условие, что трапеция – равнобедренная?
4. Задачи на построение дают возможность во всем объеме использовать как признаки, так и свойства фигур:
Вписать в данный треугольник квадрат так, чтобы одна его сторона лежала на основании треугольника, а вершины противолежащих углов на боковых сторонах треугольника.
Построить параллелограмм по:
а) двум сторонам и одной диагонали;
б) основанию, высоте и диагонали;
в) двум диагоналям и высоте.
Построить ромб по:
а) стороне и диагонали;
б) по двум диагоналям;
в) углу и диагонали, исходящей из этого угла.
Построить квадрат по:
а) сумме диагонали и стороны;
б) разности диагонали и стороны.
Построить трапецию по:
а) основанию, прилежащему к нему углу и двум непараллельным сторонам;
б) четырем сторонам;
в) основанию, высоте и двум диагоналям.
5. Систематизируя материал, связанный с конфигурациями многоугольников, можно его дополнить решением следующих задач:
Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) шестиугольника; в) восьмиугольника?
Сравните число диагоналей с числом сторон многоугольника.
Докажите, что сумма внешних углов правильного выпуклого n-угольника равна 360°.
Докажите, что центральный угол правильного многоугольника равен его внешнему углу. (Центральный угол правильного многоугольника – угол, образованный радиусами описанной окружности, проведенными к двум соседним вершинам многоугольника.)
Докажите, что в шестиугольнике, противолежащие стороны которого равны и параллельны, три диагонали, соединяющие противолежащие вершины, пересекаются в одной точке.
Докажите, что нечетные вершины правильного 2n-угольника являются вершинами правильного n-угольника.
Докажите, что середины сторон правильного n-угольника являются вершинами правильного n-угольника.
6. При рассмотрении темы «Площадь четырехугольников» следует записать все известные учащимся формулы для вычисления площадей четырехугольников. При этом полезно решить задачи по готовому чертежу.
Найдите площадь заштрихованной фигуры, используя данные рисунка (рис. 3 и 4).
Умение применять формулы для вычисления площадей различных четырехугольников можно проверить через решение задач типа:
Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
Третий этап. Тема «окружность»
Повторение на третьем этапе материала, связанного с окружностью, рекомендуется проводить в ходе решения задач. Часть работы выполняют учащиеся самостоятельно, например, по карточкам. Решение отдельных задач, которые отражают наиболее значимые геометрические факты, целесообразно продемонстрировать на доске. Предлагаемая примерная последовательность повторения предполагает, что перед каждым блоком задач учащиеся уже повторили основные определения и формулировки теоремы. Часть из доказанных в курсе теорем переформулирована в виде задач.
1. Для каждого треугольника существует вписанная в него окружность и описанная около него окружность. Полезно поставить вопрос о существовании и единственности для любой окружности вписанного или описанного около нее треугольника.
Через любые три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Дана окружность. Найдите ее центр.
Докажите, что точка пересечения двух биссектрис треугольника является центром вписанной окружности.
Найдите центр окружности, описанной около треугольника с вершинами (0; 0), (1; 2), (2; 1).
2. Для систематизации знаний учащихся о свойствах хорд следует решить задачи:
Докажите, что диаметр окружности, проходящей через середину хорды, перпендикулярен ей.
Сформулируйте и докажите теорему, обратную предыдущей.
Хорды AB и CD пересекаются в точке E. Докажите подобие треугольников ADE и CDE.
Если две дуги одной окружности равны, то стягивающие их хорды равны и равноудалены от центра окружности.
Решение следующей задачи является следствием решения предыдущей:
Докажите, что все хорды данной длины, проведенные в одной окружности, касаются некоторой другой окружности.
Докажите, что дуги, заключенные между параллельными хордами, равны.
3. Систематизируя знания о центральных и вписанных углах, можно градусную меру вписанного угла выразить через градусную меру центрального угла. Следует найти градусную меру углов, образованных хордами, секущими и касательными:
Через данную точку провести касательную к данной окружности.
Градусная мера угла, вершина которого лежит внутри круга, равна полусумме градусных мер дуг, из которых одна заключена между его сторонами, а другая между их продолжениями.
Градусная мера угла, вершина которого лежит вне круга, равна полуразности градусных мер дуг, заключенных между его сторонами.
Градусная мера угла, сторонами которого являются хорда и касательная, равна половине градусной меры дуги, стягиваемой данной хордой.
Градусная мера угла, образованного двумя касательными, равна полуразности градусных мер дуг, заключенными между точками касания.
Из конца диаметра AB проведена хорда AC, которая делит окружность на дуги, градусные меры которых относятся как 3 : 2. Вычислите величины углов треугольника ABC.
Точки A, B и C лежат на окружности. Чему равна хорда AC, если угол ABC равен 30°, а диаметр окружности 10 см?
4. Рассмотреть материал, связанный с конфигурациями, включающими в себя касательные и секущие:
Докажите, что отрезки касательных, проведенных к окружности из одной точки равны.
Из точки A, лежащей вне окружности, проведены две секущие, которые пересекают окружность в точках B1 и C1 и B2 и C2 (B1 лежит между точками A и C1, а B2 – между A и C2). Докажите подобие треугольников AB1C2 и AB2C1.
Докажите, что если из одной точки A проведены секущая, которая пересекает окружность в точках B и C (точка B лежит между точками A и C) и касательная AD, то AB•AC = AD2.
5. Систематизацию знаний учащихся по теме «Вписанные и описанные многоугольники» провести в ходе решения следующих задач:
Правильные одноименные многоугольники подобны, и их стороны относятся как радиусы вписанной или описанной окружностей.
Диагонали четырехугольника ABCD пересекаются в точке M. Докажите, что около четырехугольника можно описать окружность, если AM•CM = BM•DM.
Из точки окружности A проведены диаметр AC и равные хорды AB и AD. Докажите, что диагональ AC четырехугольника ABCD является биссектрисой его углов A и C.
6. Для индивидуальной работы можно предложить технически более сложные задачи:
Середины сторон правильного шестиугольника соединены последовательно. Докажите, что полученный шестиугольник тоже правильный. Вычислить стороны полученного шестиугольника, если сторона первоначального шестиугольника равна a
Общая хорда двух пересекающихся окружностей, равная a, служит для одной окружности стороной правильного вписанного треугольника, а для другой – правильного вписанного четырехугольника. Определите расстояние между центрами окружностей.
Около правильного треугольника со стороной a, описана окружность, около этой окружности описан квадрат, а около него – снова окружность. Определите радиус окружности, описанной около квадрата.
В окружность радиуса R вписан правильный треугольник, в который вписана окружность, а в эту окружность вписан квадрат. Найдите сторону квадрата.
7. При рассмотрении тем «Длина окружности» и «Площадь круга» полезно решить задачи по готовому чертежу.
Найдите длину границы и площадь заштрихованной фигуры, используя данные рисунка (рис. 5 и 6).
Умение применять формулы для вычисления площадей различных фигур, составленных из четырехугольников и кругов, можно проверить при решении задач типа:
Найдите площадь заштрихованной фигуры, используя данные рисунка (рис. 7).
Кроме того, полезно обратить внимание учащихся на равновеликость площадей круга, вписанного в квадрат и двух полуокружностей.