Домашние рецепты из геометрической кухни

Целью данной работы является описание дополнительных геометрических свойств треугольника. При решении целого ряда задач значительное место в программе для поступающих в вузы отводится примерам, связанным с определением площадей треугольников.

Теорема о медианах треугольника

Одной из проблем, которая не нашла отражения в школьном курсе геометрии, является доказательство равенства площадей всех шести треугольников, образованных медианами основного треугольника. Идея доказательства основана на том, что любая из трех пар смежных треугольников имеет общую высоту и равные основания, а, следовательно, и равные площади.

Теорема о медианах треугольника была сформулирована на основании личного опыта практических занятий с учениками, домашнего анализа заданий контрольных работ. Приведенное ниже доказательство может иметь конкретное применение в учебном процессе.

В курсе геометрии 8 класса (Л.С. Атанасян и др. Геометрия, 7–9) после теоремы о площади треугольника и следующих из нее следствий (п. 52) данную теорему можно рассмотреть в виде следствия или теоретической задачи, а затем применять в старших классах при решении задач типа: определить площади треугольников, на которые разбивается данный треугольник его медианами.

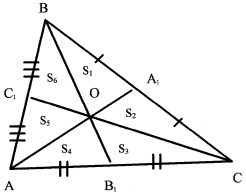
Теорема. Медианы треугольника делят его на шесть треугольников, площади которых равны.

Дано: DABC, AA₁, BB₁, CC₁ – медианы.

Доказать: S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

Доказательство I.

1. Рассмотрим DA₁OB и DA₁OC. Так как BA₁ = A₁C и высота у этих треугольников общая, то S₁ = S₂. Аналогично S₃ = S₄; S₅ = S₆.

2. Рассмотрим DABB₁ и DB₁BC. Так как AB₁ = B₁C и высота у них общая, то

   , т. е.

S₄ + S₅ + S₆ = S₁ + S₂ + S₃.

Так как S₃ = S₄, то S₅ + S₆ = S₁ + S₂.

А так как S₅ = S₆ и S₁ = S₂, то 2S₅ = 2S₁ Ю S₅ = S₁ или 2S₆ = 2S₁ Ю S₆ = S₁, и S₁= S₂ = S₅ = S₆.

Аналогично, рассмотрев  DBCC₁ и D ACC₁, получим

S₁ = S₂ = S₃ = S₄ = S₅ = S₆, что и требовалось доказать.

Доказательство II.

Так как медианы точкой пересечения делятся в отношении 2 : 1, начиная от вершины треугольника, то

OC = 2OC₁, OA = 2OA₁, OB = 2OB₁.

1. Находим

Р BOA₁ = Р AOB₁ (как вертикальные) Ю выражение (1) и S₁ = S₄; аналогично S₂ = S₅ и S₃ = S₆.

2. Рассмотрим DOBA₁ и DOCA₁; A₁B = A₁C и высота у них общая Ю S₁ = S₂.

Аналогично

что и требовалось доказать.

Разбор с учениками доказательства теоремы, приведенной здесь, показывает, что она хорошо усваивается, позволяет более глубоко понять весь комплекс математических соотношений в треугольнике.

Касательная к гиперболе

Изложенная ниже проблема возникла в процессе решения задач с применением касательной к графику функции («Алгебра, 10–11» под ред. Ш.А. Алимова). Имеющийся учебно-методический материал не исчерпывает в полной мере потенциал данной тематики. В частности, одной из проблем, которая не нашла отражения в школьном курсе, является доказательство равенства площадей всех треугольников, которые образует касательная к гиперболе

с осями координат. Эта площадь всегда равна 2| a |.

Методика доказательства проста, она основана на уравнении касательной, нахождении точек ее пересечения с осями координат и вычислении площади полученного треугольника. Приведенное ниже доказательство может иметь конкретное применение в учебном процессе. Оно может быть дано в виде теоремы, следствия или теоретической задачи сразу после изучения темы «Уравнение касательной к графику функции» или как дополнительный материал для учащихся, интересующихся математикой.

Теорема. Касательная, проведенная в любой точке графика функции

образует с осями координат треугольник постоянной площади, не зависящей от точки касания, и эта площадь равна 2| a |.

Доказательство. Пусть CB – касательная к гиперболе y = в точке A. Найдем площадь D OCB.

1. Точка касания A имеет координаты .

2. Запишем уравнение прямой CB по формуле

3. Найдем координаты точек C и B – точек пересечения прямой CB с осями Ox и Oy:

т. C:

т. B:

Так как a № 0, то 2x₀ – x = 0, x = 2x₀ и B(2x₀; 0).

4. Рассмотрим

При a < 0 ветви гиперболы расположены во II и IV квадрантах, площадь треугольника находится аналогично. Значение a берется по модулю.

Вывод: S = 2| a |, что и требовалось доказать.