Взаимообратные действия, к которым относятся вычисление производной и первообразной, должны изучаться по возможности одновременно и совместно, на одном уроке и на одной странице тетради.
Психологическая полнота ассоциации достигается в системе упражнений общностью приемов вычислений, формул, таблиц.
Первое задание – вычисление производной – дается, а второе – вычисление первообразной – проверяет решение первой задачи, так как известное в первой задаче становится неизвестным, искомым во второй задаче. За счет всего этого идет саморазвитие мысли ученика, творчество, меньше делается ошибок при вычислении первообразной, что часто бывает при раздельном изучении этих тем; кроме того, экономится время.
До одновременного изучения производной и первообразной обязательно нужно дать историческую справку о дифференциальном и интегральном исчислениях; объяснить смысл предела функции, понятия приращения функции, аргумента, понятия средней скорости изменения функции, мгновенной скорости изменения функции.
Производная
1. Определение.
Производной функции f(x) в точке x0
называется предел (если он существует) отношения
приращения функции Df(x) в этой точке к
приращению Dx аргумента, когда Dx стремится к нулю
2. Вычисление производной из определения.
или в точке x D f = f(x + Dx) – f(x).
Пример. f(x) = 
.
Найти f '(x)
Решение.
.
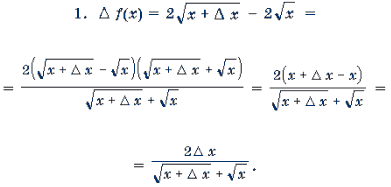
3. Правила вычисления производных.
Пример 1. f '(x) = (x2 + x + 2) ' = (x2) ' + (x) ' + 2 ' = 2x + 1 + 0 = 2x + 1.
Пример 2.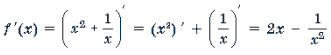 
–
или можно
(xn) ' = nxn–1.
(Доказательство методом математической индукции.)
Пример 1.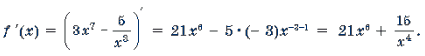 
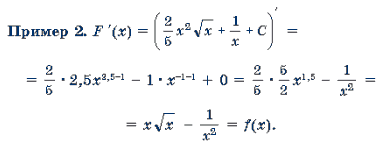
Пример 1. f '(x) = (x2(x3 + 1)) ' = x2(x3 + 1) ' + (x3 + 1)(x2) ' = x2*3x2 + (x3 + 1)*2x = 3x4 + 2x4 + 2x = 5x4 + 2x.
Пример 2. F '(x) = (2x2 – 3x + C) ' = (2x2) ' – (3x) ' + C ' = 2(x2) ' – 3(x) ' + 0 = 2*2x – 3 = 4x – 3 = f(x).
Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) имеет производную в точке x0, при этом h '(x0) = g '(f(x0))*f '(x0).
Пример 1. h(x) = (3x – 1)5, Обозначим 3x – 1 = y, тогда h(x) = y5.
y '(x) = (3x – 1) ' = 3, hy ' = 5y4.
Тогда h '(x) = 5(3x – 1)4*3 = 15(3x – 1)4 или проще h '(x) = ((3x – 1)5) ' = 5(3x – 1)4(3x – 1)' = 3*5(3x – 1)4 = 15(3x – 1)4.
Пример 2. 
Решение.
Пример 3. h(x) = (2x + 3)100,
h '(x) = ((2x + 3)100) ' = 100(2x + 3)99(2x + 3)' = 100(2x + 3)99*2 = 200(2x + 3)99.
Первообразная
1. Определение. Функция F(x) называется первообразной для функции f(x) на заданном промежутке J, если для всех x из этого промежутка выполняется равенство F '(x) = f(x).
Нахождение первообразной – интегрирование – операция, обратная операции дифференцирования.
2. Алгоритм вычисления первообразной. Любая первообразная для функции f(x) на промежутке J может быть записана в виде F(x) + C, где F(x) – одна из первообразных для функции f(x) на промежутке J, а C – постоянная.
Тогда (F(x) + C) ' = F '(x) + C ' = f(x) + 0 = f(x), т. е. F(x) + C – тоже первообразная для f(x).
Пример 1. Для функции 
на интервале (0; + Ґ) найти первообразную.
Решение. Первообразной
для 
является функция 
так как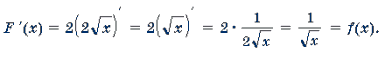 
Пример 2. Известны значения производных, найти сами функции:
( ) ' = 2; ( ) ' = x2; ( ) ' = 2x;
( ) ' = 1; ( ) ' = x3;
( ) ' = x3 + x2 + 1; ( ) ' = x + 3,5.
3. Правила нахождения первообразных.
Пример 1. f(x) = 2x + 1. F(x) – ?
Решение. 
где C может быть равно 2.
Пример 2. 
Решение. 
так как
Пример 1. 
Решение.
Пример 2. 
Решение.
Постоянный множитель можно выносить за знак производной/первообразной. Пусть k – постоянное число.
(kf) ' = k 'f + f 'k = 0*f + kf ' = kf ', т. е. (kf) ' = kf '.
F '(x) = f(x), то kF – первообразная для kf, так как (kF) ' = kF ' = kf.
Пример 1. f(x) = 5x4 + 2x. F(x) – ?
Решение.
x2(x3 + 1) + C, так как F '(x) = f(x).
Пример 2. f(x) = 4x – 3. F(x) – ?
Решение. 
Если F(x) есть
первообразная для f(x), а k и b –
постоянные, причем 
есть одна из первообразных для f(kx + b).
Если F '(x) = f(x), то по правилу нахождения производной сложной функции:
f(kx + b).
Пример 1. f(x) = 15(3x – 1)4. F(x) – ?
Решение.
(3x – 1)5 + C, так как F '(x)
= f(x).
Пример 2. 
Решение.
Для 
первообразной
является 
а функция f(x) – 
Пример 3. f(x) = 200(2x + 3)99. F(x) – ?
Исходя из рассмотренных правил и аналогично разобранным примерам составим таблицу нахождения производных и первообразных элементарных функций:
Затем изучается применение производной в физике, геометрии, для исследования функций, а также применение первообразной в вычислении площади криволинейной трапеции.
