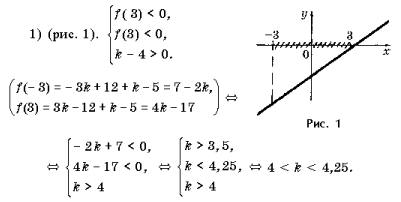
Школьная программа не предусматривает выработки прочных навыков решения задач, содержащих параметры, всеми учащимися, и более глубокое изучение возможно только на внеклассных занятиях. Нельзя дать универсальных указаний по решению задач с параметрами. Но для неравенств первой и второй степени с параметрами при заданном условии можно рекомендовать использовать графический метод решения, как более наглядный. При этом учитель может рассмотреть задачи, включающие несколько возможных случаев.
Активному и сознательному усвоению учащимися методов решения неравенств первой и второй степени с параметрами способствует актуализация знаний о свойствах линейной и квадратичной функций и их графиках.
Линейные неравенства
Определение. Функция вида y = kx + b, где k и b – произвольные числа, называется линейной функцией.
Графиком линейной функции является прямая с углом наклона к оси абсцисс равным j, где tg j = k. Если k > 0, то угол j острый; если k < 0, то угол j тупой; если k = 0, то график либо совпадает с осью абсцисс, либо параллелен ей.
Задача 1. При каких значениях k неравенство (k – 4)x + k – 5 < 0 справедливо для всех x, удовлетворяющих условию | x | Ј 3?
Решение. Пусть f(x) = (k – 4)x + k – 5. f(x) < 0; k – ?
Задача 2. Найти все значения a,
при которых для всех x, удовлетворяющих
условию | x | Ј 1, справедливо неравенство 
.
Решение.
Задача 3. При каких значениях a неравенство 2x – a2 + 5 < 0 верно при всех значениях x, удовлетворяющих условию | x | < 2?
Ответ: a < – 3; a > 3.
Задача 4. При каких значениях m неравенство (m – 2)x + 2m – 16 < 0 верно при всех значениях x, удовлетворяющих условию | x | і 5?
Ответ: m = 2.
Задача 5. При каких
значениях b неравенство 
верно при всех x,
удовлетворяющих условию | x | Ј 2?
Ответ: b < – 11, b > 1.
Неравенства второй степени
Определение.
Функция, задаваемая формулой ax2 + bx + c,
РіРґРµ a в„– 0,
называется квадратичной функцией.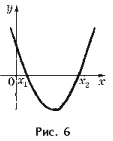
График квадратичной функции
имеет вид, изображенный на рис. 6, и называется
параболой. Точка графика с абсциссой 
называется вершиной параболы, ордината этой
точки равна
При a > 0 «ветви» параболы направлены вверх, а при a < 0 – вниз. Каждый из этих двух случаев разбивается на три подслучая в зависимости от числа корней уравнения.
При D = b2 – 4ac > 0 уравнение ax2 + bx + c = 0 имеет два действительных корня
При D = 0 уравнение имеет
один корень , задаваемый и в том числе
формулой (1).
При D < 0 уравнение не имеет действительных корней.
Рассмотрим расположение графика по отношению к оси абсцисс во всех шести случаях (рис. 7).
Задача 1. При каких значениях m неравенство mx2 – 2(m + 3)x + m < 0 верно при всех x, удовлетворяющих условию – 2 Ј x Ј 1?
Решение. Пусть f(x) = mx2 – 2(m + 3)x + m. Тогда
Задача 2. При каких a неравенство ax2 + 2(3 – 2a)x – 24 > 0 верно при всех x, удовлетворяющих условию | x | < 5?
Ответ: Ж.
Задача 3. Найдите все значения a, при которых для всех x, удовлетворяющих условию | x | Ј 3, справедливо неравенство
ax2 – 2x – a(a2 + 2) > 0.
Ответ: a < – 3.
Задача 4. При каких значениях a неравенство ax2 – x – a(a2 + 1) > 0 верно при всех x, удовлетворяющих условию | x | < 2?
Ответ: a < – 2.
Задача 5. При каких значениях a функция f(x) = – x3 + 4x2 – ax – 8 возрастает на (1; 2)?
Решение. Напишем производную от f(x) и воспользуемся критерием возрастания:
f '(x) = – 3x2 + 8x – a > 0, т. е. 3x2 – 8x + a < 0.
Пусть j(x) = 3x2 – 8x + a. Тогда имеем
Задача 6. Найдите все
значения a, при которых функция 
возрастает
для всех x О R.
Ответ: a О (– Ґ; – 3) Р(1; + Ґ).
Решение задач с параметрами в школьной практике (неравенства – один из видов таких задач) позволяет проверить:
– знание основных разделов школьной математики;
– уровень математического и логического мышления;
– первоначальные навыки исследовательской деятельности;
– перспективы возможности успешного овладения курсом математики вуза.
