| Первый день | Финал |
9.1. В числе A цифры идут в возрастающем порядке (слева направо). Чему равна сумма цифр числа 9·A?
(С. Волченков)
9.2. В стране несколько городов, некоторые пары городов соединены беспосадочными рейсами одной из N авиакомпаний, причем из каждого города есть по одному рейсу каждой из авиакомпаний. Известно, что из любого города можно долететь до любого другого (возможно, с пересадками). Из-за финансового кризиса был закрыт N – 1 рейс, но ни в одной из авиакомпаний не закрыли более одного рейса. Докажите, что по–прежнему из любого города можно долететь до любого другого.
(Д. Карпов)
9.3. Треугольник ABC вписан в окружность S. Пусть A0 – середина дуги BC окружности S, не содержащей A; C0 – середина дуги AB, не содержащей C. Окружность S1 с центром A0 касается BC, окружность S2 с центром C0 касается AB. Докажите, что центр I вписанной в треугольник ABC окружности лежит на одной из общих внешних касательных к окружностям S1 и S2.
(М. Сонкин)
9.4. Числа от 1 до 1 000 000 покрашены в два цвета – черный и белый. За ход разрешается выбрать любое число от 1 до 1 000 000 и перекрасить его и все числа, не взаимно простые с ним, в противоположный цвет. Вначале все числа были черными. Можно ли за несколько ходов добиться того, что все числа станут белыми?
(С. Берлов)
10.1. На столе стоят три пустых банки из–под меда. Винни-Пух, Кролик и Пятачок по очереди кладут по одному ореху в одну из банок. Их порядковые номера до начала игры определяются жребием. При этом Винни может добавлять орех только в первую или вторую банку, Кролик – только во вторую или третью, а Пятачок – в первую или третью. Тот, после чьего хода в какой-нибудь банке оказалось ровно 1999 орехов, проигрывает. Докажите, что Винни-Пух и Пятачок могут, договорившись, играть так, чтобы Кролик проиграл.
(Ф. Бахарев)
10.2. Найдите все бесконечные ограниченные последовательности натуральных чисел a1, a2, a3..., для всех членов которых, начиная с третьего, выполнено
(С. Волченков)
10.3. Пусть окружность, вписанная в треугольник ABC, касается его сторон AB, BC и AC в точках K, L и M соответственно. К окружностям, вписанным в треугольники BKL, CLM и AKM, проведены попарно общие внешние касательные, отличные от сторон треугольника ABC. Докажите, что эти касательные пересекаются в одной точке.
(М. Сонкин)
10.4. В квадрате n*n клеток
бесконечной шахматной доски расположены n2
фишек, по одной фишке в каждой клетке. Ходом
называется перепрыгивание любой фишкой через
соседнюю по стороне фишку, непосредственно за
которой следует свободная клетка. При этом фишка,
через которую перепрыгнули, с доски снимается.
Докажите, что позиция, в которой дальнейшие ходы
невозможны, возникнет не ранее, чем через 
ходов.
(С. Токарев)
11.1. Существуют ли 19 попарно различных натуральных чисел с одинаковой суммой цифр, таких, что их сумма равна 1999?
(О. Подлипский)
11.2. Во всех рациональных точках вещественной прямой расставлены целые числа. Докажите, что найдется такой отрезок, что сумма чисел на его концах не превосходит удвоенного числа в его середине.
(С. Берлов)
11.3. Окружность, вписанная в четырехугольник ABCD, касается его сторон DA, AB, BC, CD в точках K, L, M, N соответственно. Пусть S1, S2, S3, S4 – соответственно окружности, вписанные в треугольники AKL, BLM, CMN, DNK. К окружностям S1 и S2, S2 и S3, S3 и S4, S4 и S1 проведены общие внешние касательные, отличные от сторон четырехугольника ABCD. Докажите, что четырехугольник, образованный этими четырьмя касательными – ромб.
(М. Сонкин)
11.4. В квадрате n*n
клеток бесконечной шахматной доски расположены n2
фишек, по одной фишке в каждой клетке. Ходом
называется перепрыгивание любой фишкой через
фишку, непосредственно за которой следует
свободная клетка. При этом фишка, через которую
перепрыгнули, с доски снимается. Докажите, что
позиция, в которой дальнейшие ходы невозможны,
возникнет не ранее, чем через ходов.
(С. Токарев)
Решения задач
9.1. Заметим, что 9A = 10A – A. При вычитании этих чисел столбиком ни в одном разряде, кроме младшего, не приходится занимать единицу из следующего разряда. Таким образом, сумма цифр разности равна разности суммы цифр чисел 10A и A (которые равны) плюс 9.
Ответ: 9.
9.2. Рассмотрим некоторый путь, соединяющий некоторые два города, возможно включающий в себя некоторые закрытые после кризиса рейсы. Покажем, что в этом пути любой закрытый рейс можно заменить последовательностью незакрытых. Пронумеруем авиакомпании числами от 1 до N. В одной из авиакомпаний сохранились все рейсы: предположим, что в первой. Тогда в любой другой авиакомпании закрыли по одному рейсу. Рассмотрим только рейсы первой и второй авиакомпаний: из каждого города выходит по одному рейсу этих авиакомпаний. Следовательно, все города разбиваются на циклы. В одном из этих циклов закрыли один рейс. Очевидно, можно пролететь остальными рейсами этого цикла, следовательно, мы можем «обойти» любой закрытый рейс. Отметим, что мы при этом не используем рейсы других авиакомпаний, следовательно, аналогично можно обойтись без остальных закрытых рейсов.
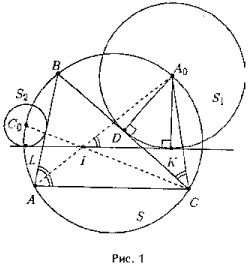9.3. Из точки I проведем
касательную IK к окружности S1 так,
чтобы луч IK пересекал меньшую дугу A0C
(см. рис. 1). Аналогичным образом проведем
касательную IL к окружности S2.
Биссектриса AI угла BAC делит дугу BC на 2 равных дуги. Поэтому точки A, I, A0 лежат на одной прямой. Аналогично, на одной прямой лежат точки C, I и C0. Из равенств
следует, что Р A0IC = Р ICA0 и A0I = A0C.
Далее, пусть D – середина отрезка BC, тогда S1 касается BC в точке D.
В прямоугольных D A0KI и D A0DC катеты A0K и A0D равны и A0I = A0C по доказанному выше. Следовательно, D A0KI = D A0DC. Отсюда Р A0IK = Р A0CD = Р A0CB. Но Р A0CB = Р A0AB (теорема о вписанном угле) и Р A0AB = Р A0AC. Значит, Р A0IK = Р A0AC, следовательно прямая IK параллельна AC. Аналогично, IL || AC, следовательно L, I, K лежат на одной прямой, параллельной AC.
9.4. Лемма. Пусть дан набор простых чисел p1,..., pn. Тогда можно за несколько перекрашиваний добиться того, что поменяют цвет те и только те числа, которые делятся на все простые числа набора.
Доказательство (по формуле включения–исключения): для каждого непустого поднабора чисел перекрасим числа, не взаимно простые с произведением всех чисел этого набора. Число, делящееся на все числа набора, перекрашивалось при каждом таком перекрашивании, всего перекрашиваний было 2n – 1, следовательно, числа, делящиеся на все числа набора перекрашены. Пусть некоторое число k не делится хотя бы на одно из чисел набора, например, на p1. Тогда оно не перекрашивалось, когда мы перекрашивали числа, не взаимно простые с p1. Остальные непустые поднаборы чисел можно разбить на пары следующим образом: поднабору, не содержащему p1, в пару ставится поднабор, полученный из него добавлением p1. При этом число k перекрашивается или при обоих перекрашиваниях пары, или ни при одном. Поэтому число k не будет перекрашено.
Лемма доказана.
Первое решение. Для каждого набора простых чисел, произведение которых не больше 1 000 000, перекрасим числа, делящиеся на все эти простые числа. По лемме такая операция возможна. Докажем, что любое число k при этом будет перекрашено. Пусть k имеет m различных простых делителей, тогда оно перекрашивалось при 2l – 1 операции, то есть нечетное число раз.
Второе решение. Назовем два числа эквивалентными, если у них совпадают наборы простых делителей. Заметим, что при наших операциях классы эквивалентности перекрашиваются целиком. Будем говорить, что один класс больше другого, если все простые делители второго класса являются делителями первого. Из леммы следует, что мы можем перекрасить любой класс, перекрасив вместе с ним только большие классы.
Сначала перекрасим минимальные классы (класс называется минимальным, если он не больше никакого другого класса). Исключим их из рассмотрения. Среди оставшихся некоторые классы станут после такого исключения минимальными. При необходимости перекрасим их и тоже исключим. И так далее.
Поскольку классов конечное число, процесс закончится.
Ответ: можно.
10.1. Пусть Винни и Пятачок вначале кладут свои орехи во вторую и третью банки, несмотря на ходы Кролика, до тех пор, пока в одной из банок не станет 1998 орехов. После этого тот, кто должен класть орехи в эту банку (пусть, например, это Винни) начинает класть их в I. При этом он уже положил во II банку не менее 999 орехов, значит, в III орехов тоже не менее 999 (туда их клал Пятачок). После этого Пятачок продолжает класть в III банку орехи, пока там не станет 1998 – это произойдет не более, чем через 500 ходов, так как в III банку также приходится класть орехи Кролику, чтобы не проиграть. После этого Пятачок также может класть орехи в I банку, так как там не более 500 орехов, положенных Винни, а Кролик вынужден будет положить орех во II или III, где их уже по 1998.
10.2. Ответ. a1 = a2 = ... = 2.
Пусть для каких–то двух членов последовательности ak и ak + 1 их НОД равен 1. Тогда
НОД(ak, ak + 1) = НОД(ak + ak + 1, ak + 1) = НОД(ak + 2 ak, ak + 1),
т. е. для всех последующих членов последовательности НОД тоже будет равен 1. При этом, начиная с k–го члена, последовательность превращается в последовательность an = an – 1 + an – 2, которая неограниченно возрастает.
Итак, НОД всегда должен быть не меньше 2. Если какие–то члены последовательности ak и ak + 1 не равны друг другу, то
ak + 2 < max{ak, ak + 1} и ak + 1 № ak + 2.
Аналогично, ak + 3 < max{ak + 1, ak + 2} < max{ak, ak + 1}.
Мы получили, что максимальное число в парах идущих подряд членов последовательности монотонно убывает, т. е. когда-то станет равным 1, и тогда НОД у каких–то членов тоже станет равен 1, что не должно случиться.
Итак, все члены последовательности должны равняться друг другу и их НОД = 2, т. е. an = 2.
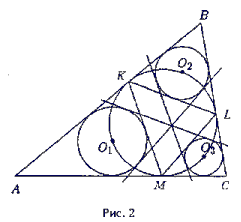10.3. Пусть K, L, M –
точки касания вписанной окружности со сторонами AB,
BC, AC соответственно, O1, O2,
O3 – центры малых окружностей (см.
рис. 2), так как
и O1 лежит на вписанной в треугольник ABC окружности. Аналогично O2 и O3 лежат на этой окружности и являются серединами дуг KL и LM. Используя результат задачи 9.3, заключаем, что построенные касательные проходят через центр окружности, вписанной в треугольник KLM, что и требовалось доказать.
10.4. Будем различать два типа ходов – внутренние и внешние, в зависимости от того, куда ставится фишка, делающая ход: внутрь исходного квадрата n * n клеток, или вне его.
Пусть получена позиция, где дальнейшие ходы невозможны, причем сделано k внутренних ходов и l внешних.
Ясно, что никакие две фишки не
находятся в соседних клетках, а в исходном
квадрате n * n не менее, чем 
клеток пусты. Так как каждый
внутренний ход увеличивал количество пустых
клеток не более, чем на 1, а каждый внешний – не
более, чем на 2, то имеем неравенство
(1)
Предположив теперь, что n
четно, разобьем исходный квадрат на
четырехклеточных квадратиков и заметим, что на
каждый квадратик пришлось не менее двух ходов, в
которых участвовали (делали ход или снимались с
доски) фишки, стоявшие в клетках этого
квадратика. Поскольку в каждом внутреннем ходе
участвовали фишки не более, чем двух квадратиков,
а в каждом внешнем – не более, чем одного, то
Из неравенств (1) и (2) получаем 
т. е. утверждение задачи в этом
случае верно.
Легко видеть, что оно верно также при n = 1 и при n = 3.
В случае n = 2m + 1, где m > 1, в «кресте», образованном третьей сверху горизонталью и третьей слева вертикалью, выделим 2m «доминошек», а остальную часть исходного квадрата разобьем на m2 четырехклеточных квадратиков. В каждом внутреннем ходе участвовать могли фишки, принадлежащие не более, чем двум из m2 + 2m рассматриваемых фигур, а в каждом внешнем – не более, чем одной. Имеем неравенство
2k + l і 2m2 + 2m, (3)
поскольку фишки каждого из квадратиков участвовали не менее, чем в двух ходах, а фишки каждой «доминошки» – по крайней мере в одном.
Из (1) и (3) следует, что 3 (k + l) і 4m2 + 4m = n2 – 1. Если здесь n2 є 0 (mod 3), то, очевидно,
Тем самым утверждение задачи полностью доказано.
11.1. Ответ. Нет.
Пусть сумма цифр каждого из чисел равна S = 9k + n, n = 0, 1, ..., 8. Тогда все эти числа имеют остаток n при делении на 9, и имеет место сравнение
19n = 18n + n є 1999 (mod 9),
откуда n є 1 (mod 9), т. е. n = 1.
1) Пусть k = 0, т. е. S = 1. Рассмотрим 5 наименьших натуральных чисел с суммой цифр, равной 1. Это числа 1, 10, 100, 1000 и 10000. Но даже их сумма больше 1999.
2) Пусть k = 1, т. е. S = 10. Рассмотрим 19 наименьших натуральных чисел с суммой цифр, равной 10. Это числа 19, 28, 37, 46, 55, 64, 73, 82, 91, 109, 118, 127, 136, 145, 154, 163, 172, 181, 190. Их сумма равна 1990 < 1999. Следующее натуральное число с суммой цифр, равной 10, есть 208, что по крайней мере на 18 больше любого из первых 19 чисел, и значит, сумма будет не менее
1990 + 18 = 2008 > 1999.
3) Пусть k і 2, т.е. S і 19. Но наименьшее число с суммой цифр не меньше 19 есть 199, а сумма любых 19 таких чисел будет заведомо больше 1999. Таким образом, мы получили, что 19 чисел, удовлетворяющих условию не существует.
11.2. Предположим
противное, т. е. существует такая расстановка
целых чисел, что для любого отрезка AB с
серединой C выполняется неравенство 
где a, b, c –
соответственно числа, стоящие в точках A, B
и C. Пусть A, B, C, An, Bn,
n = 1, 2,..., – соответственно точки – 1, 1, 
– , числовой прямой, a, b, c,
an, bn – целые числа, записанные
в этих точках. Тогда, по предположению,
и т. д. Отсюда следует, что max{a, c} > max{a1, a2} >, так как
Аналогично,
max{a1, a2} > max{a3, a4} > max{a5, a6} > ...
и
max{b, c} > max{b1, b2} > max{b3, b4} > ... .
Таким образом, a2m <
max{a, c} – m, b2m < max{b, c}
– m и, значит, при некотором m будет
выполнено неравенство a2m + b2m
Ј 2c.
Противоречие, так как число c записано в
середине отрезка A2mB2m.
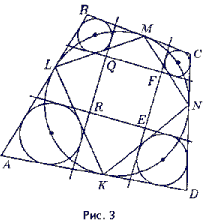
11.3. Введем обозначения (см. рис. 3). Как было показано в решении задачи 9.3, RQ || KM || EF, RE || LN || QF. Значит, образовавшийся четырехугольник – параллелограмм. Используя то, что касательные к окружности, проведенные из одной точки, равны и AB + CD = AD + BC, получаем
RQ + EF = RE + QF, так как (RQ + EF) – (RE + QF) = ( a12 + a34) – (a23 + a41),
где aij – длина общей внешней касательной к окружностям Si и Sj. Значит, RQFE – ромб.
11.4. См. решение задачи 10.4.
