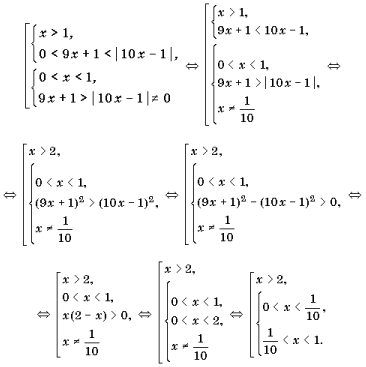
На вступительных экзаменах по математике в 1998 году абитуриентам МИРЭА предлагался билет из шести задач. В каждом билете было одно или два алгебраических уравнения и неравенства, одна задача с логарифмами, одно тригонометрическое уравнение, также одна задача по планиметрии и одна задача с параметром. Здесь мы разберем некоторые задачи, предлагавшиеся в 1998 году.
Задачи с логарифмами
Задача 1.1. Решить неравенство log x (9x + 1) < log x (| 10x – 1 |).
Решение. Способ I (классический). Так как основания логарифмов зависят от x, то для раскрытия этого логарифмического неравенства необходимо сравнивать основания с единицей.
Если основание логарифмов (x) больше единицы, то у большего логарифма – больший аргумент, и неравенство раскроется следующим образом: 0 < 9x + 1 < | 10x – 1 |;
если же основание 0 < x < 1, то у меньшего логарифма – больший аргумент, и неравенство раскроется как
9x + 1 > | 10x – 1 | > 0.
В итоге исходное неравенство равносильно совокупности систем:
Ответ: 
Способ II (нестандартный и рекомендуемый). Все утверждения и рассуждения, которые мы сделали в первом способе, можно свести к следующей системе
где сравнение основания логарифмов с единицей заложено в последнее неравенство системы как множитель (x – 1), а исходное неравенство с логарифмами предварительно было умножено на 2, чтобы избавиться от модуля. Заметим также, что нам нет необходимости писать ограничение на основание логарифмов x № 1, потому что исходное неравенство строгое (обратите внимание на задачу 2, где неравенство нестрогое).
Задача 1.2. Решить неравенство log x (6x + 1) < log x (| 7x – 1|).
Задача 2.1. Решить неравенство
log2| x | (x2 – 10x + 16) Ј log 2 | x | 7.
Решение. Домножив это
неравенство на 
сделаем следующее
преобразование:
Воспользовавшись вторым методом из предыдущей задачи, получим
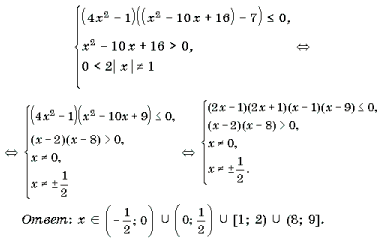
Задача 2.2. Решить неравенство
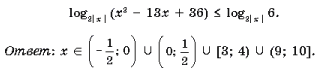
Задачи по тригонометрии
Задача 3.1. Решить уравнение sin2 17x = cos 52x + sin2 26x.
Решение. Воспользуемся
формулой понижения степени: 
Очевидные преобразования дают – cos 34x = cos 52x. (*)
Перенесем все в одну сторону и воспользуемся формулой суммы косинусов
Следует отметить, что уравнения типа (*) можно решать несколько иначе при помощи формул приведения и используя определение косинуса (или синуса, если у нас синусы). Этот метод мы рекомендуем и продемонстрируем его в следующей задаче.
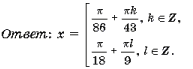
Задача 3.2. Решить уравнение sin2 14x = cos 58x + sin2 29x.
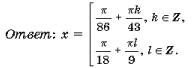
Задача 4.1. Решить уравнение sin 9x (sin 66x + cos 20x) = cos 9x (cos 66x – sin 20x).
Решение. Раскроем скобки и перегруппируем слагаемые:
sin 20x cos 9x + cos 20x sin 9x = cos 66x cos 9x – sin 66x sin 9x.
Воспользовавшись формулами «синус суммы» и «косинус суммы», получим sin 29x = cos 75x.
Применив теперь формулу
приведения, запишем уравнение в виде 
Вспомним теперь, что
изображение косинуса на «круге» симметрично
относительно оси x, потому что это проекция
радиус-вектора точки круга единичного радиуса на
эту ось. Поэтому, если cos b, то 
. Значит, 
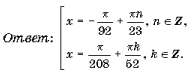
Задача 4.2. Решить уравнение sin 13x (sin 49x + cos 24x) = cos 13x (cos 49x – sin 24x).
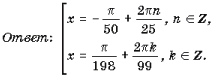
Задача 5.1. Решить уравнение cos 44x + sin4 22x = cos 38x + sin4 19x.
Решение. Способ I. Используя формулу косинуса двойного угла для cos 44x и cos 38x, получим
cos2 22x – sin2 22x + sin4 22x =cos2 19x – sin2 19x + sin4 19x.
Заметим теперь, что cos2 a – sin2 a = (cos2 a – sin2 a)•1 є (cos2 a – sin2 a)(cos2 a + sin2 a) = cos4 a – sin4 a.
С учетом этого уравнение примет вид
cos4 22x – sin4 22x + sin4 22x = cos4 19x – sin4 19x + sin4 19x Ы cos4 22x = cos4 19x Ы cos 22x = ± cos 19x.
Так как в последнем уравнении для косинусов стоит ±, то значит кроме симметрии относительно оси x добавится симметрия относительно начала координат и период корня будет не 2pn, как в предыдущей задаче, а pn.
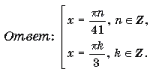
Способ II. Воспользовавшись формулами понижения степени для синуса (однократно), получим
Задача 5.2. Решить уравнение cos 60x + sin4 30x = cos 22x + sin4 11x.
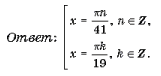
Задачи с параметром
Задача 6.1. Найти все значения параметра a, при которых данная система имеет ровно одно решение
Решение. Обратим внимание на второе уравнение системы – это уравнение прямой в отрезках. Эта прямая проходит через точки с координатами (– 80; 0) и (0; a). Теперь посмотрим на первое уравнение системы: его левая часть – это расстояние от начала координат до точки (x; y), а первое слагаемое его правой части – это расстояние от точки с координатами (– 40; 9) до точки (x; y). Перегруппировав слагаемые первого уравнения, представим его в виде
Поскольку расстояние от начала координат до точки (– 40; 9) равно 41, то по неравенству треугольника необходимые нам точки не могут лежать не на одной прямой, а точнее на луче (полупрямой) с началом в точке (– 40; 9) и направленном от начала координат по прямой, проходящей через точки (– 40; 9) и (0; 0). Этот луч можно задать следующим образом:
Теперь, нарисовав картинку, мы можем сказать, что если у исходной системы и есть решение при каком-то a, то оно единственное. Нам подходит следующий промежуток для параметра: a О [a1; Ґ), где a1 – то значение параметра, при котором точка (– 40; 9) принадлежит прямой
Подставив указанную точку в уравнение, легко находим, что a1 = 18.
В связи с уравнением (1) следует заметить, что геометрическое место точек (x; y), удовлетворяющих этому уравнению – это точки, для которых разность расстояния от них до двух зафиксированных нами точек постоянна, т. е. это одна из ветвей гиперболы (конечно, только в том случае, если эта разность меньше расстояния между взятыми точками).
Ответ: a О [18; Ґ).
Задача 6.2. Найти все значения параметра a, при которых данная система имеет ровно одно решение
Ответ: (– Ґ; – 48].
Задача 7.1. Найти все значения параметра a, при которых данная система уравнений имеет ровно два решения
Решение. Обратим внимание
на второе уравнение системы: мы сразу можем
сказать, что независимо от значения параметра a
это уравнение всегда имеет решением пару (x = 0,
y = 0). Простой подстановкой убеждаемся, что эта
пара является также решением первого уравнения
системы. Следовательно, нам нужно найти такие
значения параметра, при которых существует лишь
еще один корень. Для удобства введем следующее
обозначение: t2 = x2 + y2,
считая, что 
Система примет вид:
Из этой системы видно, что t = 0 и t = 12 являются корнями первого уравнения. Для t = 0 очевидно, что независимо от значения параметра a ему будет однозначно соответствовать решение x = 0 и y = 0, т. е. это уже найденный ранее корень. Заметим также, что если пара чисел (x; y) является решением системы, то с учетом второго уравнения пара (x; – y) тоже будет решением системы. Следовательно, поскольку у нас уже есть одно решение (0; 0), то для того, чтобы иметь ровно два решения системы, y всегда должен быть равен 0. Заметим сразу, что значение параметра a = 0 нам не подходит, так как в этом случае мы будем иметь только корень (0; 0), значит, a № 0.
Теперь у нас осталось только одно неиспользованное значение t = 12. Для нахождения соответствующих корней (x; y) и значений параметра a надо решить такую систему
Таким образом, у нас есть два параметра и соответствующие им пары корней, а именно a = 12 (x = 12, y = 0) и a = – 12 (x = – 12, y = 0). Теперь, если мы докажем, что первое уравнение системы
не имеет других корней t кроме 0 и 12, то, значит, и других параметров a, кроме найденных, больше нет (ОДЗ t О [– 12; 12]). Преобразуем уравнение к виду
Так как корень t = 12 мы уже
учли, то уравнение можно разделить на 
На области допустимых значений t (точки 0 и 12 не рассматриваются) будут выполняться следующие неравенства:
Из этих неравенств следует, что других корней t, кроме уже найденных, нет.
Ответ: a = ± 12.
Задача 7.2. Найти все значения параметра a, при которых данная система уравнений имеет ровно два решения
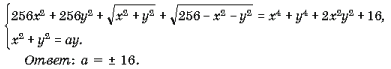
Задача 8.1. Найти все значения параметра a, при которых множество решений неравенства 2x2 – 6x + a + 16 Ј 0 (*)
непусто и содержится среди решений неравенства
x2 + 4x + a < 0. (**)
Решение. Обозначим корни
первого неравенства (*) за x1 и x2
(x1 Ј x2), а корни второго неравенства (**)
за 
Условие задачи будет выполнено,
если будут выполнены неравенства 
Это так, потому что ветви обеих парабол, стоящих в
левых частях заданных нам неравенств, направлены
вверх и область решений каждого неравенства в
отдельности находится в промежутке между его
корнями. Таким образом, задачей является
нахождение этих корней и таких значений
параметра a, при которых выполняются
установленные нами условия.
Рассмотрим сначала неравенство (**) (потому, что оно проще). Выпишем его дискриминант
Неравенство (**) имеет решен ия лишь в том случае, если a Ј 4. Итак, у нас уже есть какое-то ограничение на параметр a.
Проделаем такую же операцию с неравенством (*):
Неравенство (*) имеет решения
лишь в том случае, если 
Наше ограничение
на параметр a усилилось, и теперь будет
действовать последнее из них:
Выпишем корни для неравенств (*) и (**). Это
для (*) и
для (**). Сейчас, когда корни найдены, мы можем записать для них условия, заявленные в самом начале решения:
Теперь, перегруппировав
слагаемые 
возведем неравенство в квадрат и
изолируем корень:
(это неравенство возможно, так
как при 
корень существует и – 5 – a
> 0). Возведение этого неравенства в квадрат
дает a2 + 108a + 1152 і 0.
Решение этого неравенства с учетом ограничения
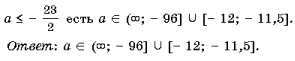
Задача 8.2. Найти все значения параметра a, при которых множество решений неравенства 2x2 – 2x + a + 15 Ј 0 непусто и содержится среди решений неравенства x2 + 6x + a Ј 0.
Ответ: a О (Ґ; – 27,5].
Задача 9.1. Найти все значения параметра a, при которых данная система уравнений имеет хотя бы одно решение
Решение. Непосредственной проверкой убеждаемся, что x = – 1 является решением второго уравнения системы для любого значения параметра a. Подставляя x = – 1 в первое уравнение, находим a, при котором x = – 1 является также решением первого уравнения:
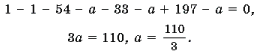
Далее, так как x = – 1 является корнем второго уравнения, то согласно теореме Безу в этом уравнении (точнее, в его левой части) можно выделить множитель x + 1. Для нахождения оставшегося второго множителя надо разделить второе уравнение на x + 1 (нацело); вот результат этой операции:
x3 – (a + 1)x2 + (a + 33)x + 1 – a = 0. (1)
Теперь вычитаем результат этого деления из первого уравнения:
x4 – 53x3 + 196 = 0.
Как видно, при этой операции параметр a из уравнения исчезает. Полученное уравнение является биквадратным, т. е. сводится к квадратному уравнению заменой y = x2, и оно имеет следующие корни: y = x2 О {4; 49}. Отсюда следует, что x О {± 2; ± 7} (т. е. четыре корня).
Остается подставить эти значения x в любое уравнение, из которого получилось только что решенное биквадратное – например, для облегчения вычислений, в уравнение третьей степени (1) и найти соответствующие им значения параметра:
x = 2 Ю 8 – 4a – 4 + 2a + 66 + 1 – a = 0,
x = – 2 Ю – 8 – 4a – 4 – 2a – 66 + 1 – a = 0,
7a = – 77, a = – 11;
x = 7 Ю 343 – 49a – 49 + 7a + 231 + 1 – a = 0,
x = – 7 Ю – 343 – 49a – 49 – 7a – 231 + 1 – a = 0, 57a = – 622,
Задача 9.2. Найти все значения параметра a, при которых данная система уравнений имеет хотя бы одно решение
