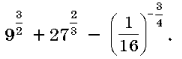
Решение первых заданий варианта
Степень с рациональным показателем и ее свойства
В большинстве заданий степени приводятся к простым основаниям, затем с помощью соответствующих свойств (во многих случаях устно) выражения упрощаются.
7. Вычислите 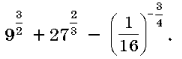
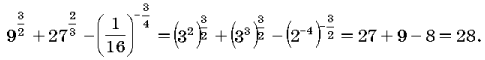
23. Упростите : ![]()
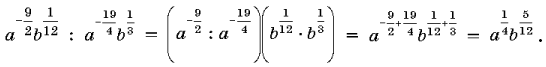
Комментарий. Знак
деления, использованный в записи задания, может
привести к некоторой путанице – запись
выражения можно понять и так: 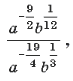 что,
естественно, изменит ответ.
что,
естественно, изменит ответ.
32. Вычислите 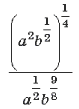 при a
= 7, b = 2.
РїСЂРё a
= 7, b = 2.
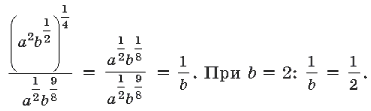
Ответ: 0,5.
46. Вычислите ![]()
![]()
Комментарий. Выполнить преобразования можно и так:
![]()
54. Вычислите 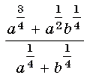 при a = 4, b = 11.
РїСЂРё a = 4, b = 11.
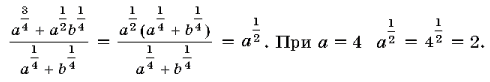
Степени и логарифмы
72. Вычислите ![]()
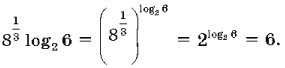
Решение неравенств методом интервалов
Во многих вариантах первое задание проверяет умение решать неравенства методом интервалов.
Метод интервалов основан на очевидном утверждении, что произведение (дробь) не изменяет знака на интервалах, на которых множители (стоящие в числителе и знаменателе) сохраняют свои знаки. Поскольку перемена знака у многочлена связана с его корнями, то интервалы знакопостоянства ограничены значениями переменной, обращающими в нуль хотя бы один из множителей. Найдя эти значения и определив знак выражения на каждом из интервалов, записываем в ответ те из них, на которых значения выражения имеют нужный знак.
2. Решить неравенство ![]()
Сначала определяем интервалы, РЅР° которых РЅРё (x – 6), РЅРё (x – 8), РЅРё (2x – 7) РЅРµ изменяют СЃРІРѕРёС… знаков. Отмечаем РЅР° координатной РїСЂСЏРјРѕР№ значения x, обращающие эти двучлены РІ нули. Рто соответственно: x = 6, x = 8 Рё x = 3,5. Точки отмечаем крестиками, показывая, что числа 6, 8 Рё 3,5 РЅРµ являются решениями. Рти точки разбивают координатную РїСЂСЏРјСѓСЋ РЅР° четыре интервала. Остается определить знак РґСЂРѕР±Рё РЅР° каждом РёР· РЅРёС… Рё записать РІ ответ те интервалы, РЅР° которых РґСЂРѕР±СЊ отрицательна.

Ответ: x < 3,5, 6 < x < 8.
Ответ можно записать и иначе: ( – Ґ; 3,5) Р(6; 8).
Комментарий. Конечно, в решении задачи столь подробное описание стандартного алгоритма излишне. Здесь достаточно было отметить на координатной прямой соответствующие точки (совершенно необязательно их отмечать крестиками), расставить знаки и записать ответ.
36. Решить неравенство ![]()
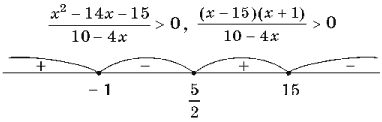
Ответ:![]()
Комментарий. Можно было и не раскладывать квадратный трехчлен на множители – достаточно было найти его корни, обозначить их на координатной оси и т.д. Кстати, нет необходимости при оформлении работы пояснять, как были найдены корни квадратного трехчлена. В данном примере их, конечно, проще было подобрать устно.
Вообще, при отыскании корней
квадратного трехчлена (ax2
+ bx + c) всегда полезно
устно проверить, нет ли среди его корней числа 1 –
в этом случае сумма коэффициентов равна нулю: (a•12 + b•1 + c = a + b + c), или числа (– 1) при этом
нулю равно выражение (a
– b + c). Второй корень
легко находится по известной формуле Виета: ![]()
64. Найдите область
определения функции ![]()
Решение. Выражение под
знаком квадратного корня может принимать только
неотрицательные значения:
x3 + 9x2 + 14x С– 0, x(x2
+ 9x + 14) С– 0, x(x + 7)(x + 2) С– 0.
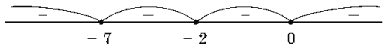
Ответ: ![]()
Решение вторых заданий варианта
Показательные уравнения
Все показательные уравнения первого раздела сводятся к простейшим показательным уравнениям или с одинаковыми основаниями в обеих частях или с 1 в правой части уравнения. В последнем случае нет нужды представлять 1 как степень с соответствующим основанием и нулевым показателем. Решения стандартны, а значит, не требуют воспроизведения теоретических фактов – так, например, можно не ссылаться на свойство монотонности, из которого следует обратимость показательной функции, позволяющая утверждать единственность корня уравнения ax = b.
2. Решите уравнение 5x + 1 + 5x + 5x – 1 = 31.
Решение. В левой части равенства вынесем за скобки 5 в наименьшей из степеней – 5x – 1:
5x – 1(52 + 5 + 1) = 31, 5x – 1 = 1, x – 1 = 0, x = 1.
Ответ: 1.
43. Решите уравнение ![]()
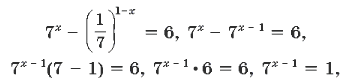
x – 1 = 0, x = 1.
Ответ: 1.
49. Решите уравнение 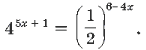
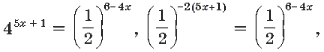
![]()
Ответ: ![]()
Комментарий. Можно,
конечно, было записать обе части в виде степеней
числа 2: 22(5x + 1) = 24x
– 6 или числа 4; ![]()
Показательные неравенства
При решении показательных неравенств определение возрастания или убывания соответствующей показательной функции является самостоятельным шагом стандартного алгоритма, поэтому он обязательно должен фиксироваться в записи решения.
21.Решите неравенство 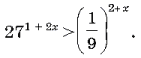
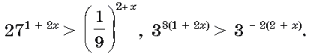 Поскольку показательная функция с
основанием (3) является возрастающей, имеем:
Поскольку показательная функция с
основанием (3) является возрастающей, имеем:
3(1 + 2x) > – 2(2 + x),
![]()
Ответ: ![]()
Комментарий. Ответ
можно записать в виде числового промежутка ![]()
23. Найдите все целые решения
неравенства ![]()
![]() Поскольку показательная функция с
основанием (5) является возрастающей, получаем:
Поскольку показательная функция с
основанием (5) является возрастающей, получаем: ![]()
Целыми решениями этого двойного неравенства являются числа: – 5, – 4, – 3, – 2, – 1.
Ответ: – 5, – 4, – 3, – 2, – 1.
45. Решите неравенство ![]()
![]() 2x – 1 < 20.
2x – 1 < 20.
Поскольку показательная функция с основанием 2 является возрастающей, получаем: x – 1 < 0, x < 1.
Ответ: x < 1.
Логарифмические уравнения
РџСЂРё решении логарифмических уравнений после освобождения РѕС‚ логарифмов (потенцирования) область определения обычно расширяется, что может повлечь Р·Р° СЃРѕР±РѕР№ появление посторонних корней, поэтому проверка корней является элементом решения. Рто, однако, РЅРµ относится Рє случаю, РєРѕРіРґР° непосредственно используется определение логарифма. Как Рё РїСЂРё решении показательных уравнений, здесь нет необходимости ссылаться РЅР° монотонность логарифмической функции для обоснования единственности решения.
12. Решите уравнение
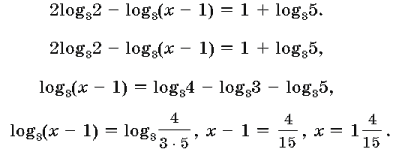
Ответ: ![]()
18. Решите уравнение log0,5(3x – 1) = – 3.
log0,5(3x – 1) = – 3. По определению логарифма,
3x – 1 = 0,5 – 3, 3x – 1 = 8, x = 3.
Ответ: 3.
Комментарий. Несколько хуже было представлять (– 3) как log0,58.
74. Решите уравнение
log23 – log2(2 – 3x) = 2 – log2(4 – 3x).
log23 – log2(2 – 3x) = 2 – log2(4 – 3x),
log23 + log2(4 – 3x) = log24 + log2(2 – 3x),
log23(4 – 3x) = log24(2 – 3x),
12 – 9x = 8 – 12x,
Проверка корня:
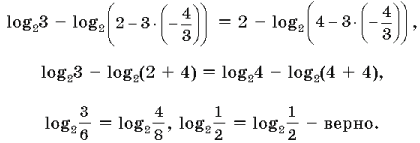
Комментарий.
1) Проверка корня здесь является обязательным элементом решения, в отличие от рассмотренных в вариантах 12 и 18 случаев применения определения логарифма.
2) Можно было сразу потенцировать, получая пропорцию:
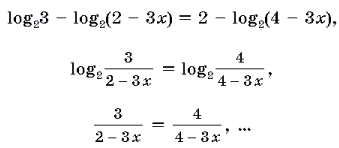
Логарифмические неравенства
При решении логарифмических неравенств установление факта возрастания или убывания соответствующей логарифмической функции является самостоятельным шагом стандартного алгоритма, и он обязательно должен фиксироваться в записи решения. При этом, как и при решении показательных неравенств, излишне ссылаться на сам теоретический факт – например, «поскольку основание логарифмической функции – число 0,25 меньше 1, функция убывающая».
Во многих случаях при потенцировании добавляется ограничение, накладываемое областью определения логарифма, что приводит к двойному неравенству.
32. Решите неравенство 2lg6 – lgx > 3lg2.
Решение. 2lg6 – lgx > 3lg2, lg62 – lg23 > lgx,
![]() поскольку логарифмическая
функция с основанием 10 возрастает, с учетом ее
области определения получаем:
поскольку логарифмическая
функция с основанием 10 возрастает, с учетом ее
области определения получаем: ![]()
Ответ: ![]()
58. Решите неравенство log0,25(3x – 5) > – 3.
Решение. log0,25(3x – 5) > – 3, log0,25(3x –
5) > log0,250,25 – 3,
поскольку логарифмическая функция с основанием
0,25 убывает, получаем: ![]()
Комментарий. Можно записывать вместо двойного неравенства систему неравенств:
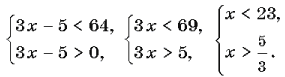
71. Решите неравенство log6(5x – 2) > 3log62 + 2.
log6(5x – 2) > 3log62 + 2, log6(5x – 2) > log623 + log662,
log6(5x – 2) > log6288. Поскольку логарифмическая функция с основанием 6 возрастает, получаем: 5x – 2 > 288, x > 58.
Ответ: x > 58.
Третье задание
Решение тригонометрических уравнений на заданном промежутке
Третье задание варианта проверяет знание основных фактов тригонометрии. При этом тригонометрические формулы знать полезно, но совсем не обязательно – они приведены в приложении к Cборнику, и ими можно пользоваться даже на экзамене.
Во многих случаях нужно найти корни довольно простого тригонометрического уравнения, принадлежащие заданному промежутку. Как правило, это отрезок [0; 2p]. В этих заданиях удобнее пользоваться изображением тригонометрического круга или графиком соответствующей функции, а не выписывать общую формулу решения соответствующего простейшего уравнения, с последующим «выуживанием» из нее подходящих значений.
7. Найдите все решения уравнения (sin x + cos x)2 = 1 + sinx cosx, принадлежащие отрезку [0; 2p].
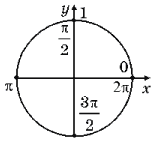 Решение.
Решение.
(sinx + cosx)2 = 1 + sinxcos x,
sin2x + 2sinxcosx + cos2x = 1 + sinxcosx,
1 + 2sinxcos x = 1 + sinx•cos x, sinxcosx = 0.
Решениями являются и нули синуса, и нули косинуса.
Отметим их на тригонометрическом круге:
Ответ: ![]()
18. Найдите корни уравнения ![]() принадлежащие отрезку [0; 2p].
принадлежащие отрезку [0; 2p].
Решение. 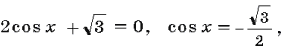
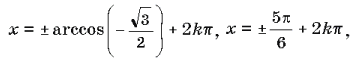 где k – целое число.
где k – целое число.
При ![]() – не принадлежит
заданному отрезку.
– не принадлежит
заданному отрезку.
При ![]() - не принадлежит
заданному отрезку.
- не принадлежит
заданному отрезку.
При других целых k корни не принадлежат отрезку [0; 2p].
Ответ: ![]()
Комментарий. Полезно сравнить это решение с решением предыдущей задачи.
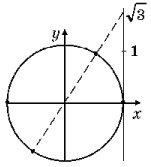 69. Найдите все решения уравнения
69. Найдите все решения уравнения ![]() ,
принадлежащие отрезку [0; 2p].
,
принадлежащие отрезку [0; 2p].
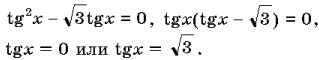
Ответ: ![]()
Решение тригонометрических уравнений
13. Решите уравнение 4cos2x – 1 = 0.
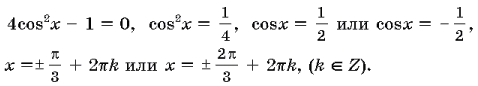
Ответ: ![]() .
.
Комментарий. Можно применить формулу понижения степени
2cos2x – 1 = сos2x, 4cos2x – 1 = 0,
2(2cos2x – 1) + 1 = 0,
Ответ: ![]()
26. Решите уравнение ![]()
Решение. ![]()
x = – p + 4pk (k О Z).
Ответ: – p + 4pk (k О Z).
Комментарий. Можно (но
необязательно) в ответе вынести за скобки : ![]()
Тригонометрические тождества
Обычно одну из частей заданного равенства с помощью формул удается преобразовать к виду, который имеет другая часть, но иногда удобнее оказывается действовать иначе.
81. Докажите тождество ![]()
Рмеем: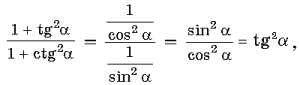 что Рё требовалось
доказать.
что и требовалось
доказать.
Комментарий. Несколько проще было предварительно умножить данное равенство на 1 + ctg2a:
1 + tg2a = tg2a (1 + ctg2a).
Далее tg2a (1 + ctg2a) = tg2a + tg2a ctg2a = tg2a + 1, что и требовалось доказать.
33. Докажите тождество ![]()
Доказательство. Достаточно
доказать, что тождеством является равенство ![]()
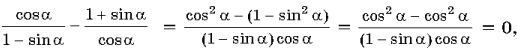
что и требовалось доказать.
Комментарий. Еще проще доказать тождественность произведений:
(1 – sina)(1 + sina) = cos2a,
(1 – sina)(1 + sina) = 1 – sin2a = cos2a.
Нахождение значения одной из тригонометрических функций по заданному значению другой
В этих заданиях, используя тригонометрические формулы, с учетом знака в заданном промежутке, выражают искомую функцию через данную, затем подставляют данное значение и производят вычисления.
14. Найдите cosx, если ![]()
В указанном промежутке 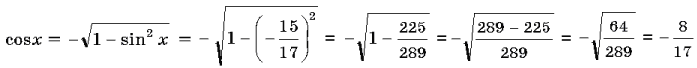
Форма и содержание материала соответствуют публикации Г. Муравина в газете «Педагогический поиск» (спецвыпуск 1999 г.).