13. Функция y = f(x) задана
своим графиком. Укажите:Решение четвертых заданий варианта
Среди четвертых заданий, в основном, представлены два типа: описание свойств функции по ее данному графику и изображение графика функции по ее описанию. Некоторые из этих заданий могут быть рассмотрены при повторении свойств функций еще до знакомства с исследованием функций с помощью производной.
При определении свойств функций по их графикам ответы предполагаются приближенными, однако, в записи это отражать не обязательно.
13. Функция y = f(x) задана
своим графиком. Укажите:
а) область определения функции;
б) при каких значениях x функция y не имеет производной;
в) при каких значениях x f '(x) < 0, f '(x) > 0;
г) наибольшее и наименьшее значения функции;
д) в какой точке графика касательная к нему параллельна оси абсцисс.
Ответ:
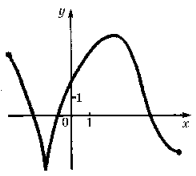
а) область определения функции: [ – 3,5; 6];
б) функция не имеет производной на концах промежутка [ – 3,5; 6] и в его внутренней точке x = – 1,5;
в) f '(x) < 0 при – 3,5 < x < – 1,5 и при 2,5 < x < 6, f '(x) > 0 при – 1,5 < x < 2,5;
г) наибольшее значение функции (4,5), наименьшее значение функции (– 3);
д) график имеет касательную, параллельную оси абсцисс, в точке (2,5; 4,5).
37. Функция y = f(x) задана
своим графиком. Укажите:
а) область определения функции;
б) при каких значениях x f(x) Ј 0,5;
в) точки экстремума функции;
г) промежутки возрастания и промежутки убывания функции;
д) наибольшее и наименьшее значение функции.
Ответ:
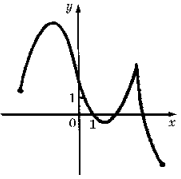
а) область определения функции: [ – 3,5; 5];
б) f(x) Ј 0,5 при x = 1,5 и при 4 Ј x Ј 5;
в) точки экстремума функции: x = – 1,5 и x = 3,5 – точки максимума, x = 1,5 – точка минимума;
г) промежутки возрастания: [ – 3,5; – 1,5] и [1,5; 3,5], промежутки убывания: [ – 1,5; 1,5] и [3,5; 5];
д) наибольшее значение функции 5,5; наименьшее: – 3.
Построение графика, обладающего заданными свойствами
При выполнении этих заданий полезно придерживаться следующей схемы. Сначала по информации, содержащейся в пунктах а) и б), выделить прямоугольник, в котором заключен искомый график, затем обозначить промежутки возрастания и убывания, точки максимума и минимума функции, отметить известные точки графика, и только затем провести искомую кривую.
3.4. Изобразите график непрерывной функции, зная, что:
а) область определения функции есть промежуток [– 3; 4];
б) значения функции составляют промежуток [ – 2; 5];
в) в левом конце области определения функция принимает наибольшее значение;
г) 2 – единственная точка экстремума функции.
Ответ. График может выглядеть, например, так, как показано на рисунке.
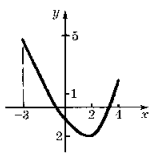Комментарий. Функция
непрерывна и, поскольку в левом конце области
определения она принимает свое наибольшее
значение, то, во-первых, это значение равно 5,
во-вторых, единственный экстремум – минимум, и он
же является наименьшим значением функции, равным
– 2.
В пункте в) не утверждается, что функция только в левом конце области определения принимает свое наибольшее значение. Так, например, данная функция «имеет право» принять свое наибольшее значение и в правом конце области определения. Чтобы исключить эту возможность, пункт в) должен звучать так: «свое наибольшее значение функция принимает в левом конце области определения».
6. Изобразите график непрерывной функции, зная, что:
а) область определения функции есть промежуток [– 5; 2];
б) значения функции составляют промежуток [– 2; 5];
в) промежутки убывания функции [– 5; – 2] и [0; 2];
г) функция возрастает на промежутке [– 2; 0];
д) отрицательные значения функция принимает только в точках промежутка (1; 2].
Ответ: см. рисунок.
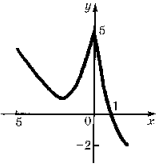Комментарий. Наибольшее
значение, равное 5, функция может принимать
при x = – 5 и (или) при x = 0. Поскольку только на
промежутке (1; 2] значения непрерывной функции
отрицательны, то x = 1 – нуль функции.
15. Изобразите график функции, зная, что:
а) область определения функции есть промежуток [– 2; 5];
б) значения функции составляют промежуток [– 5; 3];
в) производная функции положительна на (2; 5), отрицательна на (– 2; – 1) и на (– 1; 2);
г) нули производной функции: – 1 и 2;
д) нули функции: 0 и 3.
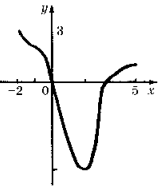Ответ:
Комментарий. В условии не сказано, что функция непрерывна, однако, поскольку во всех внутренних точках области определения функция имеет производную, «оторваться» могут только «крайние» точки. Но можно изобразить и график непрерывной функции. Знаки производной позволяют определить промежуток убывания [ – 2; 3] и возрастания [3; 5]. В точке x = 3 функция имеет минимум. При переходе через свой нуль при x = – 1 производная не меняет знак. Можно (хотя и вряд ли целесообразно) изобразить график разрывной функции, обозначив «выколотые» точки кружочками.
70. Изобразите график функции y = f(x), зная, что:
а) область определения функции есть промежуток [– 5; 4];
б) значения функции составляют промежуток [ – 4; 5];
в) f '(x) > 0 для любого x из промежутка ( – 1; 2), f '(x) < 0 для любого x из промежутка ( – 5; – 1) и (2; 4), f '(x) = 0 при x = 2;
г) нули функции: – 1 и 3.
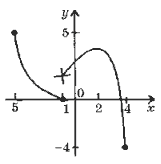Ответ.
Комментарий. В пункте в) по сути сказано, что при x = – 1 производная функции не существует (поскольку ни положительное, ни отрицательное, ни нулевое значение она в этой точке не принимает). Функция в этой точке может, например, иметь разрыв.
Нахождение производной данной функции
В этих заданиях применяются формулы производных и правила дифференцирования.
5. Найдите производную функции f(x) = 2x2 + tgx.
Решение. 
Угловой коэффициент касательной
В части четвертых заданий фигурирует угловой коэффициент касательной к графику функции. Поскольку он равен значению производной, то решение сводится к нахождению производной по формулам и вычислению ее значения.
11. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = x – lnx в его точке с абсциссой x = 3.
Решение. 
Ответ: 
22. Дана функция f(x) = 2x2 – x + 1. Найдите координаты точки ее графика, в которой угловой коэффициент касательной к нему равен 7.
Решение. f ' (x) = (2x2 – x + 1) ' = 4x – 1, f '(x) = 7, 4x – 1 = 7, 4x = 8, x = 2;
y = 2•4 – 2 + 1 = 7.
Ответ: (2; 7).
24. Дана функция 
Найдите координаты точек ее графика, в которых
касательные к нему параллельны оси абсцисс.
Решение. Касательная, проведенная к графику функции в некоторой его точке, параллельна оси абсцисс, если:
1) ее угловой коэффициент (значение производной в этой точке) равен нулю,
x = – 2 или x = 2.
2) эта точка не лежит на оси абсцисс,
Ответ: 
67. Найдите производную функции f(x) = x3lnx.
Ответ: f '(x) = x2(3lnx + 1).
Комментарий. Последнее преобразование – вынесение за скобки x2 – выполнять не обязательно, можно оставить в ответе f '(x) = 3x2lnx + x2.
Промежутки возрастания, убывания функции
Для нахождения промежутков возрастания или убывания функции используются достаточные условия – на промежутке, где производная больше нуля, функция возрастает, где меньше нуля – убывает. Следует помнить, что если, например, производная больше нуля на (a; b), а функция непрерывна на [a; b], то промежуток ее возрастания [a; b].
При выполнении таких заданий, сначала находим производную данной функции, затем определяем, на каких промежутках она принимает положительные, а на каких отрицательные значения, и, наконец, записываем промежутки возрастания и (или) убывания.
16. Найдите промежутки возрастания функции f(x) = 3x3 – 3x2 + 5.
f '(x) = ( 3x3 – 3x2 + 5) ' = 9x2 – 6x. f '(x) > 0: 9x2 –6x > 0,
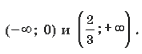
Поскольку f(x) –
непрерывная функция, она возрастает на
промежутках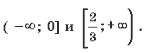 
Ответ: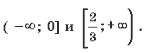
Комментарий. Решение
неравенства fR(x) > 0 можно было
записать как объединение числовых промежутков: 
. Однако аналогичная запись промежутков
возрастания функции является ошибкой, уже в силу
своей бессмысленности – определения
возрастания функции на объединении промежутков
не давалось.
Наибольшее и наименьшее значения функции на промежутке
Стандартный способ нахождения наибольшего и наименьшего значений непрерывной функции на промежутке заключается в вычислении ее значений на концах промежутка и в критических точках внутри промежутка с последующим выбором наибольшего и наименьшего из них. Однако, когда заданная функция является квадратичной, можно использовать полученные в основной школе знания ее свойств.
20. Найдите наименьшее значение функции f(x) = 3x2 + 18x + 7
на промежутке [ – 5; – 1].
Решение 1. Найдем критические точки функции: f '(x) = (3x2 + 18x + 7) ' = 6x + 18.
Производная существует при всех значениях x.
f '(x) = 0, 6x + 18 = 0, x = – 3 – единственная критическая точка внутри заданного промежутка [ – 5; – 1].
f( – 5) = 2, f( – 1) = – 8, f( – 3) = – 20 – наименьшее значение.
Решение 2. Графиком данной
функции является парабола, ветви которой
направлены вверх, а наименьшее значение функции
равно ординате вершины параболы. Вершина имеет
абсциссу, равную 
Число – 3 входит в
заданный промежуток, значит, наименьшее значение
функции на промежутке [ – 5; – 1] равно f( – 3) = –
20.
Ответ: – 20.
Решение пятых заданий варианта
В пятых заданиях продолжается начавшаяся в четвертых заданиях линия производных. Добавляются задачи на нахождение первообразных и вычисление площадей криволинейных трапеций.
25. Какие из данных функций возрастают на всей области определения: y = sinx, y = x + 1, y = ex ?
Функция y = sinx убывает,
например, на промежутке 
,
остальные функции являются возрастающими: y =
x + 1 – линейная функция с положительным угловым
коэффициентом, y = ex – показательная
функция с основанием большим единицы, 
– по свойствам квадратныx корней.
Ответ: y = x + 1, y = ex,
Комментарий. Обосновать
возрастание функции можно,
опираясь на свойства неравенств: из обеих частей
неравенства с положительными членами можно
извлечь квадратные корни: 
Рассматривая
a и b как произвольные значения аргумента функции , получаем, определение возрастающей
функции: x1 > x2 Ю f(x1)
> f(x2).
41. Какие из данных функций убывают на всей области определения: y = 3x + 2, y = – 5x + 9, y = x2, y = – x3 + x ?
Решение. y = 3x + 2 – возрастает, как линейная функция с положительным угловым коэффициентом, y = – 5x + 9 – убывает как линейная функция с отрицательным угловым коэффициентом, y = x2 – возрастает при x і 0.
Производная функции y = –
x3 + x: y ' = – 3x2 + 1
положительна, например, на промежутке 
, значит, на этом промежутке функция y = –
x3 + x возрастает.
Ответ: y = – 5x + 9.
15. Найдите точки экстремума функции f(x) = 2x3 – 3x2 – 1.
Решение. f '(x) = (2x3 – 3x2 – 1) ' = 6x2 – 6x. Производная существует при всех значениях x, значит в точках экстремума она равна нулю: 6x2 – 6x = 0, x(x – 1) = 0, критические точки x = 0 и x = 1.
При переходе через 0 производная меняет знак с « + » на « – », значит 0 – точка максимума. При переходе через 1 производная меняет знак с « – » на « + », значит, 1 – точка минимума.
Ответ: Точка максимума x = 0, точка минимума x = 1.
Задания с использованием понятия первообразной
1. Найдите все первообразные функции f(x) = x4 + 3x2 + 5.
Ответ: 
Комментарий. Можно записать ответ иначе:
Любая из первообразных имеет
вид: 
34. Найдите функции, производной которых является функция f(x) = 2x + x2.
Решение. Нужно найти все первообразные функции f(x).
Ответ: 
В некоторых заданиях из множества первообразных нужно выбрать ту, график которой проходит через заданную точку.
21. Найдите первообразную функции f(x) = 3x – 5, график которой проходит через точку (4; 10).
График искомой первообразной
проходит через точку (4; 10), значит, F(4) = 10,
Ответ: 
28. Является ли функция F(x) = x3 + 3x – 5 первообразной для функции f(x) = 3(x2 + 1)?
Решение 1. Найдем производную функции F(x). Если она совпадет с даной функцией f(x), то F(x) – первообразная f(x), если нет – не первообразная.
F '(x) = (x3 + 3x – 5)' = 3x2 + 3 = 3(x2 + 1) = f(x).
Ответ: F(x) является первообразной для f(x).
Решение 2. Любая
первообразная для f(x) имеет вид 
Взяв С равным – 5, получим F(x).
32. Является ли функция F(x) = x4 – 3x2 + 1 первообразной для функции f(x) = 4x3 – x2 + x?
Решение. F '(x) = ( x4 – 3x2 + 1)' = 4x3 – 6x № f(x).
Ответ: F(x) не является первообразной для f(x).
Площадь криволинейной трапеции
При выполнении заданий следует изображать криволинейную трапецию.
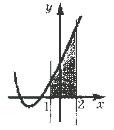5. Найдите площадь фигуры,
ограниченной графиком функции f(x) = x2
+ 5x + 6, прямыми x = – 1, x = 2 и осью абсцисс.
Изобразим криволинейную трапецию.
Найдем какую-нибудь
первообразную функции f(x) = x2 + 5x
+ 6: 
Найдем площадь криволинейной трапеции как приращение этой первообразной:
Ответ: 28,5.
Комментарий.
В этой задаче достаточно схематического
изображения соответствующей параболы – по
графику, собственно, нужно увидеть, что на
промежутке [ – 1; 2] функция f(x) принимает
только положительные значения. Для этого в
данном случае проще всего указать корни.