А. Правдин,
пос. Пижма,
Нижегородская обл.

Еще раз о замечательных точках треугольника

Теорема 1. Точка пересечения высот остроугольного треугольника ABC делит его высоту BB₁ на отрезки, отношение которых, считая от вершины, равно

.

Доказательство.

1)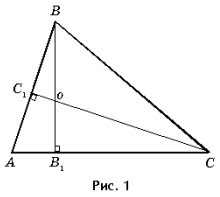 D BC₁O – прямоугольный, и (рис. 1)

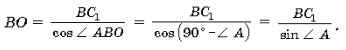
2) D BC₁C – прямоугольный, и

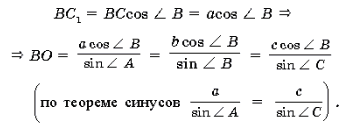
3)

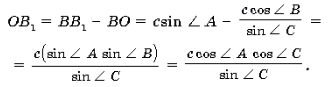
4)

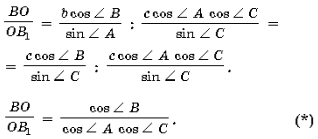
Замечание. Если один из углов тупой, то в (*) соответствующий косинус нужно взять по модулю.

Теорема 2. Если O – точка пересечения биссектрис треугольника ABC, то

где AA₁ – биссектриса угла A, AB = c, BC = a, CA = b (рис. 2).

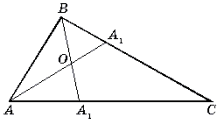Доказательство. 1) В D ABC AA₁ – биссектриса РA, поэтому AB : AC = BA₁ : CA₁ = BA₁ : (BC – BA₁) и

2) В D ABA₁ BO – биссектриса Р B, поэтому AO : OA₁ = BA : BA₁

и 

1. Расстояние от вершины до ортоцентра

Из 2) доказательства теоремы 1 следует, что

(для треугольников произвольных по виду) или

Пример 1. Найти расстояние от вершины B треугольника ABC до ортоцентра, если 

По теореме косинусов Тогда 

Поэтому BO = 9.

2. Расстояние от вершины до точки пересечения биссектрис треугольника (ицентра, центра вписанной окружности)

Из теоремы 2 следует, что

Так как   то получим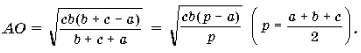

Можно доказать, что AO² = bc – 4Rr.

Пример 2. В треугольнике ABC AB = 8 см, BC = 7 см, CA = 6 см. Найти расстояние от точки A до точки пересечения биссектрис.

Решение. Найдем биссектрису угла A: AA₁ = 6 см.

1. Между центром вписанной окружности и точкой пересечения медиан (центр тяжести) – рис. 3.

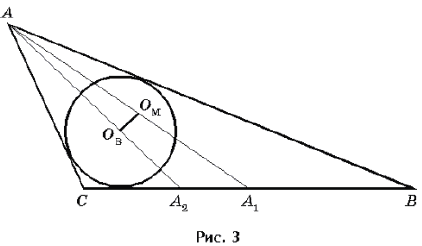
Способ I (векторный). Пусть

1) По свойству медиан имеем

2) Из (**) следует, что AO_B : O_BA₂ = (b + c) : a, поэтому AO_B : AA₂ = (b + c) : (b + c + a). По свойству биссектрисы треугольника AC : AB = CA₂ : A₂B, тогда

Следовательно,

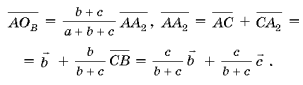
Тем самым получим

3) Из рис. 3 

4) Так как скалярный квадрат вектора равен квадрату его длины 2bccos a = b² + c² – a²,

и можно получить равенство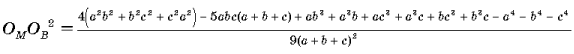

Одним из упрощений равенства будет

Пример 3. AC = 6, AB = 8, BC = 7. Найти расстояние между центром вписанной окружности и точкой пересечения медиан.

Решение. Из теоремы 2 следует, что

AO_B : O_BA₂ = 14 : 7 = 2 : 1

и  OA_B : AA₂ = 2 : 3.

По свойству биссектрисы треугольника AC : AB = CA₂ : A₂B,

тогда

Следовательно,

Тогда 

Так как скалярный квадрат вектора равен квадрату его длины и 2bccos a = 51, то

Ответ:

Замечание. В данном примере можно было сделать вывод, что O_MO_B C A₁A₂, так как OA_B : AA₂ = 2 : 3 = AO_M : AA₁ и поэтому .

Способ II. 1) Найти медиану

2) Найти биссектрису

3)

4) В DA₁AA₂ известны длины всех сторон, поэтому можно найти cos F A₁AA₂.

5) В D O_MAO_B по теореме косинусов можно найти O_MO_B.

Пример 4. AC = 9, AB = 18, BC = 21. O_MO_B – ?

Решение. 1) Медиана

2) Биссектриса

3) 

4)

5) В D O_MAO_B по теореме косинусов OMOB2 = .

Ответ: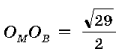

2. Между центром описанной окружности и точкой пересечения медиан (центр тяжести)

O – центр описанной окружности, OM – точка пересечения медиан, A₁ и C₁ – середины сторон соответственно AB и BC (рис. 4 и 5).

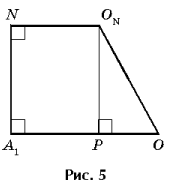
1) В D C₁KB   

Тогда CK=a-0,5c cos b

2)  D CC₁K подобен D CO_MN. Тогда CN : CK = NO_M : KC₁ = 2 : 3,

поэтому 

3) Из 2)

4) F A = a, тогда F COB = 2a, поэтому F COA- = a, OA₁ = Rcos a.

5)

6) В D OPO_M по теореме Пифагора

Известно, что 2accos b = a² + c² – b², 2bccos a = b² + c² – a² (теорема косинусов);

Пример 5. Стороны треугольника AB = 30, BC = 28, CA = 26. Найти расстояние между центром описанной около треугольника окружности и точкой пересечения медиан.

Решение. 1) Найдем площадь треугольника по формуле Герона,

2) sin b = .

3) В D C₁KB  BC₁ = 15, C₁K = 12, KB = 9, тогда CK = 19.

4) D CC₁K подобен њ CO_MN. Тогда  CN : CK = NO_M : KC₁ = 2 : 3,

поэтому

5)

6)

7) В D OPO_M по теореме Пифагора

Ответ:

3. Между центром описанной окружности и центром вписанной окружности

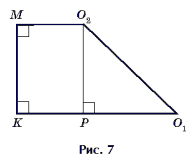
O₁ – центр описанной, O₂ – центр вписанной окружностей (рис. 6 и 7).

1) F A = a, F CO₁B = 2a, поэтому F BO₁K = a, O₁K = Rcos a и

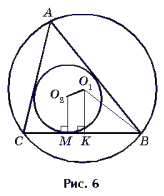
2) Так как O₂ – центр вписанной окружности, то O₂M = r.

3) Так как из точек A, B, C проведены по две касательные к описанной окружности, то отрезки касательных, концами которых являются точки касания и вершины треугольника, равны и можно показать, что BK = p – b.

Поэтому

4) O₁P = Rcos a – r.

5) В D O₁PO₂ (рис. 7) по теореме Пифагора имеем

O₁O₂² = O₁P² + O₂P = O₁P² + KM²,

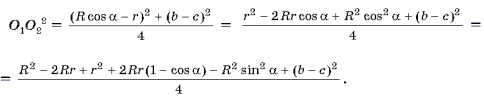
Упростим

Тем самым формула Эйлера O₁O₂² = R² – 2Rr.