Избранные параграфы из книги
«Математика, 5. учебник-собеседник»

§ 53. Математика событий. Перечисляем варианты размещения по порядку

В § 42 вы решали задачи 1 и 2 о Гришиных гостях и о гвоздиках в вазах2. Перечитайте еще раз те задачи. В них было неважно, в каком порядке перечисляются предметы: гости в одном рейсе, или гвоздики в одной вазе. Например, если в хрустальной вазе гвоздика вишневого цвета, а две другие – в фарфоровой вазе, то можно сказать: «алая и белая в фарфоровой» или «белая и алая в фарфоровой» – это будет один и тот же вариант. Но часто бывает важно указать, в каком именно порядке располагаются или следуют друг за другом предметы. Так, важен порядок, в котором идут цифры в записи числа, буквы в слове: 12 и 21 – разные числа, НО и ОН – разные слова.

! Приведите и вы какие-нибудь примеры того, когда важно указать порядок расположения предметов.

В § 15 мы специально обсуждали разные варианты расположения по порядку одних и тех же предметов (помните?). Порядок может оказаться важен и при перечислении вариантов событий. Решим такую задачу.

Задача. Алеша, Боря, Витя и Гриша на даче Гришиного дедушки решили устроить соревнование по бегу. Дедушка объявил, что он установил два приза: за 1-е место – большую шоколадку, за 2-е – маленькую. Надо перечислить все варианты распределения бегунов по призовым местам.

Рисунок: Алеша, Боря, Витя и Гриша бегут по направлению к дедушке, который держит в руках две шоколадки – большую и маленькую.

Чтобы решить задачу, давайте рассуждать. Кто-то из четверых станет победителем соревнования; сколько здесь возможностей? Каждому ясно, что 4. Ведь обязательно произойдет одно из четырех событий: 1-м прибежит Алеша, 1-м прибежит…

! Продолжите список этих событий.

При каждом победителе кто-нибудь из оставшихся троих станет 2-м призером. Например, если 1-й призер – Алеша, то 2-м призером может оказаться Боря, Витя или Гриша. Чтобы записать все варианты, договоримся обозначить участников соревнования первыми буквами их имен и писать буквы в порядке занимаемых мест. Например, запись БА означает, что 1-й призер Боря, 2-й – Алеша. Тогда получаются варианты:

АБ, АВ, АГ, если 1-й призер – Алеша;
БА, БВ, БГ, если 1-й призер – Боря;
ВА, ВБ, ВГ, если 1-й призер – Витя;
ГА, ГБ, ГВ, если 1-й призер – Гриша.

Видим, что здесь возможны 12 вариантов.

• А если располагать по порядку занятых мест не двоих призеров, а всех участников соревнования, то сколько получится вариантов?

Это разумный вопрос. И его можно задать не только для четырех участников, но и для любого их числа. И не обязательно интересоваться только участниками какого-либо соревнования. И даже не обязательно интересоваться именно людьми. Располагать по порядку можно любые предметы, и ответ на вопрос «Сколькими вариантами можно расположить по порядку n предметов?» полезно знать для любого n. В 6-м классе мы найдем формулу, дающую ответ на него. А в этом параграфе обсудим случаи, когда n = 2 и n = 3.

__________

Начнем со случая n = 2. Представьте, например, очередь из двух человек. Сколько вариантов их размещения в очереди? Каждому ясно, что таких вариантов 2 .

2 варианта размещения двух человек – мужчины и женщины – в очереди у окошка кассы.

Конечно, вместо людей в очереди можно размещать друг за другом (реально или мысленно) любые предметы, например, две разные буквы или две разные цифры. Ответ всегда будет один и тот же: 2 варианта. В начале параграфа мы уже приводили примеры таких вариантов для букв Н, О и цифр 1, 2.

Теперь обсудим случай, когда n = 3.

! Подумайте и скажите, сколькими вариантами можно разместить по порядку 3 предмета.

Нетрудно перечислить все возможные варианты. Их 6.

Рисунок: 6 вариантов размещения по порядку трех матрешек разного размера.

Чтобы записать эти варианты, проще всего, пожалуй, размещать по порядку 3 разные буквы или 3 разные цифры. Используем, например, буквы А, Б и В (можно представить, что, как и раньше, ими обозначены Алеша, Боря и Витя, финиширующие в соревнованиях по бегу или стоящие друг за другом в очереди). Тогда получаются следующие варианты:

АБВ, АВБ, БАВ, БВА, ВАБ, ВБА.

Будем называть цепочкой знаков всякую запись, в которой какие-то знаки (например, буквы или цифры) расположены в определенном порядке. Записывать цепочкой можно, конечно, не только знаки, но и названия предметов, имена людей и многое другое. Во всех таких случаях мы ради краткости будем говорить просто
«цепочка». Если в цепочке все знаки встречаются по одному разу, т. е. не повторяются, то такую цепочку назовем цепочкой без повторений.

Так, интересующие нас варианты размещения по порядку трех предметов записаны выше в виде шести трехбуквенных цепочек без повторений. Если же для ответа на тот же вопрос использовать, например, цифры 1, 2 и 3, то получатся записи в виде шести цепочек из трех цифр:

123, 132, 213, 231, 312, 321 .

L Это перечислены трехзначные числа с цифрами 1, 2 и 3?

Да, эти записи можно прочитать и как записи чисел, но не всех трехзначных чисел с цифрами 1, 2, 3, а только тех, где каждая цифра используется по одному разу. Но когда интересуются просто цепочками цифр, принято читать такие записи: один-два-три, один-три-два, … .

! Продолжите чтение этих шести вариантов для цифр 1, 2, 3.

Конечно, записывая варианты размещения по порядку трех предметов, не обязательно использовать именно эти цифры или именно эти буквы.

! Назовите такие же варианты размещения цифр 2, 5, 7. Запишите все трехбуквенные цепочки без повторений из букв Б, В, Г.

Теперь можно было бы обсудить случай n = 4. Но мы отложим это до § 65, где обсудим одно полезное общее правило подсчета числа вариантов.

53.1. Что такое цепочка знаков? Какая цепочка называется цепочкой без повторений?
53.2. Сколькими вариантами можно расположить по порядку 2 предмета; 3 предмета?
53.3. а) У Ани и ее родителей такой обычай: кто-то из них заваривает чай, причем утренний и вечерний «дежурные» различны. Члены этой семьи договорились менять каждый день вариант распределения обязанностей утреннего и вечернего дежурных. Смогут ли они не повторять такие варианты в течение недели?

Для подкрепления ответа запишите все такие варианты (например, обозначив Аню буквой А, а ее родителей – буквами О и М).

б) Изменим условие задачи а), добавив к нему, что в чаепитии принимает участие приехавшая погостить Анина бабушка, и она тоже будет одним из дежурных. Смогут ли члены семьи при этом условии не повторять варианты в течение 10 дней?

Рисунок: стол, за которым Аня, ее родители и бабушка пьют чай.

Для подкрепления ответа запишите все такие варианты, используя подходящие буквы.

в) (У) Младший брат Смекалкина решил задачу а) и придумал задачу с измененным условием: Аня и ее родители устраивают чаепитие трижды в день и дежурные по чаю за день не повторяются. Он предложил Смекалкину написать все варианты распределения обязанностей утренних, дневных и вечерних дежурных. Смекалкин сказал, что можно не записывать эти варианты, а воспользоваться тем, что было сделано в объяснительном тексте. Там говорилось точно о таком же распределении, когда перечислялись варианты размещения по порядку трех предметов. И все полученные варианты были записаны там несколько раз: при помощи разных букв и разных цифр.

Посмотрите еще раз объяснительный текст этого параграфа и убедитесь в правоте Смекалкина. Какие буквы и какие цифры использовались там для записи вариантов? Придумайте сами задачу, которая решалась бы записью тех же вариантов.

53.4. Дача Гришиного дедушки находится недалеко от пруда. У дедушки есть лодка, в которой могут разместиться все четверо друзей: Алеша, Боря, Витя и Гриша. Дедушка разрешил им покататься на лодке. Один из мальчиков будет гребцом, один – рулевым. Друзья захотели перепробовать все варианты распределения между ними ролей гребца и рулевого.

Рисунок: пруд; четыре мальчика (Алеша, Боря, Витя и Гриша) плавают на лодке: один гребет, один – рулевой, двое – пассажиры.

а) Успеют ли мальчики осуществить свое намерение, если им разрешено кататься 1 час, а на каждый вариант они решили отвести 5 минут?

б) (У) Младший брат Смекалкина стал решать задачу а) и начал записывать варианты распределения двух ролей между Алешей, Борей, Витей и Гришей. Но Смекалкин сказал, что записывать варианты для этой задачи вовсе не обязательно. Ведь в ней получаются точно такие же варианты, что и в задаче из объяснительного текста; надо только заменить 1-го призера гребцом, а 2-го – рулевым. Так что сразу ясно, что всех вариантов здесь тоже 12.

Обдумайте эту догадку Смекалкина, а потом решите устно похожую задачу с измененным условием: Гриша повредил руку и не может быть гребцом, и мальчики решили отвести на каждый вариант 8 минут; успеют ли они перебрать все такие варианты за 1 час?

в)* (У) Представьте, что Гриша не может быть гребцом, а Алеша не хочет быть рулевым. Успеют ли мальчики осуществить все варианты, возможные при этих условиях, если им разрешено кататься полтора часа и на каждый вариант они решили отвести 12 минут?

53.5. В объяснительном тексте появились трехбуквенные цепочки. Точно так же можно говорить о двухбуквенных цепочках, четырехбуквенных и т. д. Двухбуквенные цепочки без повторений из букв А, О, М вы записали, выполняя задание 53.3 а).

а) Сколько всего двухбуквенных цепочек без повторений из букв В, О, П, Т ? Догадайтесь, как можно узнать ответ, не записывая эти цепочки. (Совет: сравните это задание с задачей из объяснительного текста.) Затем запишите эти цепочки. Сколько среди них оказалось слов русского языка? Подчеркните их.

б) Найдите как можно больше пар букв, для которых каждая из двухбуквенных цепочек без повторений – слово русского языка. Сравните ваш список таких пар со списком, составленным соседом по парте. Оказались ли у кого-нибудь из вас слова, которые не нашел другой?

53.6. Из букв Л, Ш, Ю можно составить 6 трехбуквенных цепочек без повторений:

ЛШЮ, ЛЮШ, ШЛЮ, ШЮЛ, ЮЛШ, ЮШЛ.

Как вы видите, из них одна цепочка (ШЛЮ) – это слово русского языка.

а) Запишите все трехбуквенные цепочки без повторений из букв К, О, Т. Сколько среди них слов русского языка? Подчеркните их.

б) Подберите такие 3 буквы, чтобы среди трехбуквенных цепочек без повторений из этих букв было 2 слова русского языка. Проверьте, правильно ли выполнил это задание сосед по парте.

в) (У) Укажите такие 3 буквы, чтобы среди трехбуквенных цепочек без повторений из этих букв не было ни одного слова русского языка.

53.7. В очереди в школьный буфет стоят ученики в таком порядке: Боря, Галя, Аня, Дима, Витя.

а) Трое учеников ушли из очереди. Кто за кем остался стоять в очереди? Перечислите все варианты возможного ответа. (Совет: как и раньше, для краткости записи вариантов можно обозначить учеников первыми буквами их имен.)

б) Двое учеников ушли из очереди. Кто за кем остался стоять в очереди? Перечислите все варианты возможного ответа.

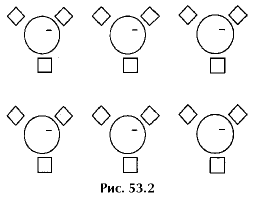
53.8о. а) Аля, Боря и Витя рассаживаются вокруг круглого стола. На приведенных ниже рисунках укажите все возможные варианты их размещения за круглым столом, вписав в прямоугольные рамочки первые буквы имен каждого из них.

б) Если интересоваться только тем, кто у каждого из ребят будет соседом слева, а кто – соседом справа, то вариантов окажется меньше. Выполнив задание а), отметьте на рисунке 53.2 одним и тем же номером те варианты, которые не отличаются взаимным расположением соседей. Сколько оказалось номеров?

Ответ: _______________________ .

Комментарии к вопросам и заданиям из § 53

53.1. Ответ на этот вопрос легко получить из соответствующего абзаца объяснительного текста параграфа. Он может звучать так: цепочкой знаков называется всякая запись, в которой какие-то знаки расположены в определенном порядке. Если в цепочке все знаки встречаются по одному разу, т. е. не повторяются, то она называется цепочкой без повторений.

53.2. Ответы на оба вопроса даны в объяснительном тексте. Здесь может быть 2 случая: учитель удовлетворен только указанием количества вариантов, либо потребует развернутого объяснения, как это количество получается.

53.3. а) Ответ: не смогут. В неделе 7 дней, а вариантов распределения утреннего и вечернего дежурств только шесть: АМ, МА, АО, ОА, МО, ОМ.

б) Ответ: смогут. Имеется 12 вариантов распределения утреннего и вечернего дежурств: АМ, МА, АО, ОА, МО, ОМ, АБ, БА, ОБ, БО, МБ, БМ.

53.4. а) Ответ: успеют. Имеется 12 вариантов распределения роли гребца и рулевого. В этом проще всего убедиться, если воспользоваться предложением Смекалкина из пункта б) этого задания.

б) В этом пункте сначала обсуждается принципиально важное положение, что перечисление вариантов не зависит от того, что именно фигурирует в этих вариантах – призовые места или роли в лодочном экипаже. Как отмечено в комментарии к заданию 42.7, такое обсуждение формирует у учащихся важное понятие, которое в математике принято называть комбинаторной схемой.

Ответ на задание, содержащееся во второй части этого пункта, отрицателен: не успеют. Легко подсчитать, что в данных условиях имеется 9 вариантов распределения ролей гребца и рулевого. Для этого нужно догадаться, что требуемые варианты получаются из вариантов, записанных при выполнении пункта а), вычеркиванием тех из них, где гребцом выступает Гриша. Таких вариантов 3. Если подобное рассуждение будет трудно восприниматься школьниками, можно попросить их выписать все возможные в данных условиях варианты. Вот перечень этих вариантов: АБ, АВ, АГ, БА, БВ, БГ, ВА, ВБ, ВГ.

в) Ответ: успеют. Действительно, в этом случае будет только 7 нужных вариантов – их список получается из перечня вариантов, составленного в пункте б), вычеркиванием тех вариантов, в которых Алеша выступает рулевым. Таких вариантов два: БА и ВА.

53.5. а) Ответ: 12 цепочек. Вот их список: ВО, ОВ, ВП,ПВ, ВТ, ТВ, ОП, ПО, ОТ, ТО, ПТ, ТП. Подчеркнуты слова русского языка, их 4.

б) Мы можем указать 12 таких пар:

АД и ДА, АЗ и ЗА, АН и НА, АХ и ХА, ИЛ и ЛИ, ИМ и МИ, ИН и НИ, ОН и НО, ОТ и ТО, УС и СУ, УФ и ФУ, ЯЛ и ЛЯ.

Комментировать большинство слов предъявленного списка нет нужды; напомним лишь, что СУ – мелкая французская монета, ИН – это (согласно «Толковому словарю русского языка» С.И. Ожегова и Н.Ю. Шведовой, 4-е изд. – М., 1998) то же самое, что АН, а АН – противительный союз, указывающий на то, что происходит нечто неожиданное, противоположное тому, что ожидалось.

53.6. а) КОТ, КТО, ОКТ, ОТК, ТКО, ТОК. Подчеркнуты 3 слова русского языка.

б) Можно взять, например, буквы Н, О, С. Среди трехбуквенных цепочек без повторений из этих букв будет 2 слова русского языка: СОН и НОС.

в) Можно взять, например, любые 3 согласные.

53.7. а) Возможны 10 вариантов: БГ, БА, БД, БВ, ГА, ГД, ГВ, АД, АВ, ДВ.

б) И здесь возможны 10 вариантов: БГА, БГД, БГВ, БАД, БАВ, БДВ, ГАД, ГАВ, ГДВ, АДВ.

Сильным учащимся можно предложить подумать над тем, почему число вариантов в пунктах а) и б) оказалось одинаковым. Можно ли было предвидеть это до перечисления всех вариантов? Ответ – да, так как и в том, и в другом случае речь идет о числе способов выбора двух учеников из пяти: при этом можно считать, что в задании а) выбираемая пара учеников остается в очереди, а в задании б) такая пара из очереди уходит.

Полезно также сопоставить эту задачу с задачей 42.3.

53.8. а) Уже не раз учащиеся видели, что имеется 6 вариантов расположения трех предметов по порядку. В данном случае эти 6 вариантов вписываются в прямоугольные рамочки, заготовленные на рис. 53.2.

б) Разглядывая отмеченные в пункте а) варианты, легко убедиться, что имеются 2 различных расположения, отвечающих условиям из б). Они задаются цепочками АБВ и АВБ. Ответ: потребуются 2 номера.

§ 54. Математика событий. Цепочки, в которых знаки могут повторяться

В предыдущем параграфе мы перечисляли цепочки без повторений, состоящие из букв или цифр. Но нередко приходится иметь дело с цепочками, в которых одинаковые знаки могут повторяться. Например, в слове оно буква О встречается дважды; в слове мама каждая из двух букв встречается дважды.

! Укажите несколько слов, в которых какая-то буква встречается трижды.

Конечно, и среди чисел есть много таких, в записи которых одинаковые цифры встречаются более одного раза.

Цепочки, в которых одинаковые знаки могут повторяться, появляются при решении многих задач на перечисление вариантов. Вот одна из самых простых таких задач.

Задача 1. Перечислите все двузначные числа, в записи которых используются цифры 1, 2 и 3.

Числа, о которых говорится в задаче, можно разбить на 3 группы: начинающиеся с цифры 1, начинающиеся с цифры 2, начинающиеся с цифры 3. Числа в каждой группе легко перечислить: в первой группе – 11, 12, 13; во второй – … , в третьей – …

! Перечислите числа во второй и третьей группах.

Список чисел, полученный при решении задачи 1, пригодится для решения следующей задачи.

Задача 2. Перечислите все трехзначные числа, в записи которых используются цифры 1, 2 и 3.

Такие числа снова можно разбить на 3 группы в зависимости от того, какая цифра стоит первой. Первая группа состоит из чисел, начинающихся с цифры 1. Рассмотрим эти числа. В записи каждого из них вторая и третья цифры составляют цепочку. Перечислить все такие цепочки – то же самое, что перечислить все двузначные числа, в записи которых участвуют цифры 1, 2 и 3. А вы уже перечислили их, когда решали задачу 1. Значит, первая группа интересующих нас чисел такова:

111,   112,   113,
121,   122,   123,
131,   132,   133.

! Перечислите числа во второй и третьей группах.

54.1. а) Запишите все трехбуквенные цепочки из букв Л и И. Сколько среди них слов русского языка? Подчеркните их.

б) Подберите другие две буквы так, чтобы среди трехбуквенных цепочек из этих букв было 2 слова русского языка.

њ в)* Можно ли подобрать две буквы так, чтобы среди составленных из них трехбуквенных цепочек с возможными повторениями оказалось 3 слова русского языка? њ

54.2. а) Перечитайте в объяснительном тексте § 42 условие задачи о гостях, приезжающих к Грише, и посмотрите таблицу, которая там была составлена. Для решения той задачи можно составить и другую таблицу – с тремя столбцами. В клетках первого столбца будем записывать номер рейса, которым приехал Алеша, в клетках второго столбца – номер рейса, которым приехал Боря, в клетках третьего – номер рейса, которым приехал Витя. Обозначим эти столбцы буквами А, Б, В. Вот как будут выглядеть первые три строки новой таблицы, в которых записаны первые три варианта:

Таблица 28

Начертите в тетради таблицу для всех восьми вариантов и заполните ее.

б) Перечислите все трехзначные числа, в записи которых участвуют только цифры 1 и 2.

в) Обратите внимание, как похожи решения в задачах а) и б): ведь можно сказать, что в строках таблицы из а) записаны все трехзначные числа с цифрами 1 и 2. Запишите теперь все двузначные числа с цифрами 1 и 2 и придумайте такую задачу на перечисление вариантов, чтобы в строках таблицы для ее решения «прочитывались» бы эти двузначные числа.

54.3. а) Перечислите все трехбуквенные цепочки из букв А и М, в которых нет рядом стоящих одинаковых букв.

б) Перечислите все трехзначные числа с цифрами 1 и 2, в которых нет рядом стоящих одинаковых цифр.

54.4. В записи натуральных чисел первая цифра не может быть нулем. Поэтому, например, цепочка 012 не может быть прочитана как трехзначное число.

а) Перечислите трехзначные числа, которые можно составить из цифр 0, 1, 2.

б) Каких чисел больше: трехзначных, составленных из цифр 1, 2, 3, или четырехзначных, составленных из цифр 0, 1, 2 ?

54.5. Прочитывая номер какого-нибудь телефона, люди обычно разбивают цепочку цифр этого номера на группы, по 2 или 3 цифры в каждой группе. Например, шестизначный номер 275275 можно представить в виде 27-52-75 или в виде 275-275. При первом варианте его читают «двадцать семь, пятьдесят два, семьдесят пять»; при втором варианте – «двести семьдесят пять, двести семьдесят пять».

Кнопочный телефонный аппарат.

Для запоминания какого-нибудь номера иногда стоит подумать, как удобнее разбить его на группы. Для номера, который мы только что рассмотрели, удобнее, конечно, второй вариант: надо просто повторить два раза одно и тоже число. А для номера 223242 удобнее, пожалуй, первый вариант: 22-32-42.

Как, по вашему мнению, удобнее разбить следующие номера, чтобы легко их запомнить?

501502;   434241;    254025;   537735

Запишите ваши варианты; сравните их с вариантами, предложенными соседом по парте; обсудите с ним (или с кем-нибудь из старших) свой выбор. њ

54.6*. а) Клоун объявил, что у него 6-значный номер телефона. А запоминать его незачем, потому что можно сразу назвать его, если помнить очень простое свойство цепочки цифр этого номера: она получается, если записать подряд 4 числа, из которых каждое последующее в 4 раза больше предыдущего.

Определите этот номер. Объясните, почему других 6-значных номеров с тем же свойством нет.

б) Младший брат Смекалкина отгадал загадку клоуна, а затем решил немного изменить ее: в свойстве цепочки цифр номера он заменил условие «в 4 раза больше» условием «на 4 больше». Смекалкин, поразмышляв, сказал, что у этой загадки получается несколько отгадок.

Найдите все цепочки из 6 цифр, которые могут получиться, если записать подряд 4 числа такие, что каждое последующее на 4 больше предыдущего. Объясните, почему других цепочек из 6 цифр с тем же свойством нет.

54.7^о. Рассмотрите полоску из 2-х клеток. 

Каждая ее клетка может быть закрашена или не закрашена . Вот все возможные варианты раскраски двухклеточной полоски.

а) На приведенных ниже трехклеточных полосках укажите все возможные варианты их раскраски (лишние заготовки полосок, если таковые окажутся, перечеркните).

б) Выполните то же задание, что и а), для полоски, состоящей из 4 клеток.

в) (У) Сравните количество раскрашенных полосок в задании а) с количеством трехзначных чисел, записанных с помощью цифр 1 и 2 (см. задание 54.2, б). Попытайтесь объяснить совпадения этих чисел.

54.8. Рассмотрите полоску из 3-х клеток.

Каждая ее клетка может быть закрашена или не закрашена . Вот все варианты закрашивания ее клеток так, что нет соседних закрашенных клеток и нет соседних незакрашенных клеток.

а)^о На приведенных ниже четырехклеточных полосках укажите все возможные варианты такой же закраски клеток (лишние заготовки полосок, если таковые окажутся, вычеркните).

б) Выполните то же задание, что и а), для полоски, состоящей из 5 клеток.

Комментарии к заданиям из § 54

54.1. а) Вот список требуемых цепочек:

ИИИ, ИИЛ, ИЛИ, ИЛЛ, ЛИИ, ЛИЛ, ЛЛИ, ЛЛЛ.

Подчеркнуты 2 слова русского языка.

б) Годятся, например, буквы К и О; соответствующие слова КОК и ОКО. Другой пример: буквы И и М; соответствующие слова ИМИ и МИМ.

в) Нет, нельзя. Мы не считаем, что от учащихся надо требовать полное обоснование этого ответа, поскольку для такового необходим довольно большой перебор возможностей. Для читателей-энтузиастов, желающих досконально разобраться в обсуждаемом задании, оценим величину этого перебора. Искомая оценка будет основываться на следующих наблюдениях.

1) В трехбуквенном слове русского языка, состоящем из двух букв, обязательно одна буква гласная, а другая согласная (буквы й, ь, ъ отсутствуют). В частности, нет трехбуквенных слов, состоящих из одной буквы. Это означает, что среди восьми трехбуквенных цепочек, составленных из двух букв, только 6 могут быть «кандидатами» в слова русского языка.

2) Согласно правилам русского языка, слова не могут начинаться с буквы Ы и в них не бывает две буквы Ы подряд. Значит, букву Ы нужно исключить из рассмотрения.

3) Согласно правилам русского языка, в словах не может быть дважды буква Ё. Прямым перебором легко убедиться, что среди цепочек вида – какая-либо согласная буква, нет ни одного слова русского языка. Тем самым, букву Ё из рассмотрений нужно исключить.

4) Аналогично наблюдению 3 исключается буква Э.

5) Поскольку буквы Х, Ц, Ч, Ш, Щ в трехбуквенных словах не могут быть удвоенными, перебором их сочетаний с гласными легко убедиться, что данные буквы также нужно исключить из рассмотрения.

Теперь, когда число рассматриваемых гласных букв сократилось до 7, а согласных – до 15, подсчитаем число вариантов выбора двух букв, из которых будут строиться цепочки. По правилу произведения таких вариантов 105. Это не такое уж большое число, и если в классе учится 30 человек, то каждому достанется просмотреть 3–4 варианта. При этом в большинстве вариантов не потребуется рассматривать все 6 комбинаций трехбуквенных цепочек, в которых фигурируют обе выбранные буквы. Из первого наблюдения вытекает, что если среди трехбуквенных цепочек, составленных из двух букв, встречаются 3 слова русского языка, то по крайней мере в одном из них есть две одинаковые рядом стоящие буквы. Поэтому в первую очередь надо рассматривать именно такие цепочки. В подавляющем большинстве случаев эти цепочки не будут словами русского языка. В тех нескольких случаях, когда получается какое-то слово русского языка (например, РЕЕ – предложный падеж слов РЕЙ и РЕЯ), нельзя указать два слова требуемого типа из тех же букв.

Задание а) мы рекомендуем обсудить в классе, задание б) выполнить дома. Задание в), фигурирующее в учебнике в качестве дополнительного, моделирует своеобразное математико-лингвистическое исследование и представляет собой приглашение продвинутых в математическом отношении учащихся к размышлениям на подобные темы. Демонстрация таких неожиданных для них применений математики в других областях знания повышает их познавательную активность и способствует развитию творческого потенциала таких учеников.

54.2. б) Вот эти числа:

111,  112,  121,  122,   211,  212,  221,  222.

в) В данном пункте еще раз обсуждается принципиальное положение, что перечисление вариантов не зависит от того, какие объекты фигурируют в этих вариантах.

Приведем список требуемых двузначных чисел: 11, 12, 21, 22. Учащимся, которым трудно придумать задачу на перечисление вариантов с таким ответом, можно предложить видоизменить задачу из объяснительного текста § 42 про Гришиных гостей.

54.3. Оба пункта этого задания мы рекомендуем выполнить в классе.

а) 2 цепочки: АМА и МАМ.

б) 2 числа: 121 и 212.

После выполнения задания полезно обсудить, почему совпало количество вариантов, и как варианты, перечисленные в б), могут быть получены из вариантов, перечисленных в а).

54.4. а) 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221, 222. Всего 18 чисел.

б) Четырехзначных чисел, составленных из цифр 0, 1, 2, ровно вдвое больше: их 54; трехзначных чисел, составленных из цифр 1, 2, 3, только 27.

54.5. Удобные для запоминания разбиения таковы 501-502; 43-42-41; 25-40-25; 537-735 (в последнем случае приемлем и вариант 53-77-35).

54.6. а) Номер телефона клоуна 141664. Других 6-значных номеров с тем же свойством нет, так как если записать подряд 4 числа, из которых каждое последующее в 4 раза больше предыдущего, и начать не с 1, то получится число не менее чем из 7 цифр. Можно предложить сильным учащимся дополнительный вопрос: сколько существует 7-значных номеров с тем же свойством?

б) Все цепочки из 6 цифр с требуемым свойством таковы: 261014, 371115, 481216, 591317. Чтобы убедиться, что других таких цепочек из 6 цифр нет, нужно записать подряд 4 числа такие, что каждое последующее на 4 больше предыдущего; тогда 6-значное число получится, если первые два числа однозначные, а два других – двузначные.

54.7. а) При правильном выполнении задания останется одна лишняя заготовка.

б) Здесь останется две лишних заготовки.

в) Если закрашенную клетку полоски обозначить 1, а незакрашенную – 2, то сразу становится ясно, почему вариантов закраски полоски столько же, сколько трехзначных чисел, записанных с помощью цифр 1 и 2.

54.8. Легко понять, что раскраска полоски полностью определяется тем, закрашена ее первая клетка или нет. Поэтому в обоих пунктах задания имеется 2 варианта раскраски указанных там полосок.