Турнир математических боев

В рамках Открытого тренировочного турнира математических боев для школьных команд, организуемого Московским Центром Непрерывного Математического Образования, в воскресенье 22 октября, был впервые проведен тур для семиклассников. В нем приняли участие восемь команд из шести школ Москвы и области. На решение задач этого тура (учитывая возрастные особенности) школьникам было отведено 2,5 часа. В это время, на совещании руководителей команд были определены пары для предстоящих боев.

Следует подчеркнуть, что организаторы турнира преследуют прежде всего учебные цели, то есть учащиеся имеют возможность потренироваться в коллективном решении и содержательном обсуждении нестандартных задач. В турнире не выявляются абсолютные чемпионы и аутсайдеры, но определяются победители каждого конкретного боя, поэтому существенным является подбор максимально равноценных пар команд для каждого боя.

При подготовке заданий, в которой (помимо авторов) приняли участие Л.Н. Бирюков, С.С. Бирюкова и А.В. Спивак, были использованы материалы Костромского и Пермского областных турниров математических боев.

1. Можно ли сложить сплошную стенку, имеющую форму параллелепипеда с размерами 9ґ15ґ16, из кирпичей размером: а) 3ґ5ґ7; б) 2ґ5ґ6, если ломать кирпичи нельзя, но можно поворачивать?

Решение. а) В число, выражающее объем стенки, не входит множитель 7, а в число, выражающее объем кирпича, этот множитель входит. Следовательно, объем стенки не может делиться на объем кирпича нацело, то есть, стенку сложить нельзя.

б) Грань стенки выкладывается из граней кирпичей. Каждая из граней кирпича имеет четную площадь. Грань стенки с размерами 9ґ15 имеет нечетную площадь, поэтому не может быть сложена из данных кирпичей. Следовательно, стенку сложить нельзя.

2. Можно ли разрезать торт, украшенный 12 розочками, четырьмя прямолинейными разрезами на куски так, чтобы на каждом куске оказалось ровно по одной розочке?

Решение. Докажем, что четыре прямые не могут разбить плоскость более, чем на 11 частей. Известно, что любая прямая делит плоскость на две полуплоскости. Рассмотрим две прямые а и b на плоскости. Если а || b, то эти прямые делят плоскость на три части, так как все точки одной прямой лежат в одной полуплоскости относительно другой. Если прямые а и b пересекаются, то они делят плоскость на четыре части. Следовательно, большее количество частей получится, если никакие две прямые (из четырех) не будут параллельны. Если третья прямая c проходит через точку пересечения а и b, то образуется шесть частей, а если не проходит – то семь (для доказательства достаточно рассмотреть полуплоскости c границей с). Следовательно, четыре прямые, по которым должны осуществляться разрезы, должны пересекаться только попарно. Учитывая это условие, проведем четвертую прямую. Получим еще четыре части, то есть, наибольшее количество частей, на которые четыре прямые делят плоскость, равно 11.

Ответ. Нельзя.

3. Даны две дроби: . Укажите какую-нибудь пару натуральных значений m и n так, чтобы разность между данными дробями принимала наименьшее возможное положительное значение.

Решение. Рассмотрим и преобразуем выражение с учетом того, что 77 и 13 – взаимно простые числа:

Если числа m и n – натуральные, то наименьшее значение дроби достигается, если модуль числителя равен 1. Это возможно, например, при m = 6; n = 1.

4. Винни-Пух съедает 3 банки сгущенки и банку меда за 25 минут, а Пятачок – за 55 минут. Одну банку сгущенки и 3 банки меда Пух съедает за 35 минут, а Пятачок – за 85 минут. За сколько минут они совместно съедят 6 банок сгущенки?

Решение. Из условия следует, что 4 банки сгущенки и 4 банки меда Пух съедает за 60 минут, а Пятачок – за 140 минут. Значит, одну банку сгущенки и одну банку меда Пух съедает за 15 минут, а Пятачок – за 35 минут. Используя первое из условий, получим, что 2 банки сгущенки Пух будет есть 10 минут, а Пятачок – 20 минут. Так как Пух ест сгущенку в два раза быстрее Пятачка, то за 20 минут они съедят 6 банок сгущенки.

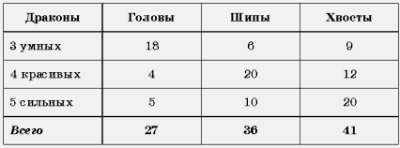
5. У драконов может быть разное количество голов, шипов и хвостов, но у каждого дракона не меньше одной головы, двух шипов и трех хвостов. Дракон считается умным, если голов у него больше, чем шипов и хвостов, вместе взятых; красивым, если шипов больше, чем голов и хвостов, вместе взятых; сильным, если хвостов больше, чем голов и шипов, вместе взятых. Собрались вместе 3 умных, 4 красивых и 5 сильных дракона. Каково наименьшее возможное суммарное количество: голов; шипов; хвостов?

Решение. Из условия задачи следует, что у умного дракона не меньше, чем 6 голов, у красивого – не меньше, чем 5 шипов, у сильного – не меньше, чем 4 хвоста. Наименьшее количество голов, шипов и хвостов для трех умных, четырех красивых и пяти сильных драконов указано в таблице.

6. В каждой клетке доски 99 ґ 99 сидит жук. В некоторый момент времени каждый жук переполз на соседнюю (по горизонтали или по вертикали) клетку. Верно ли, что после этого на доске останется хотя бы одна пустая клетка?

Решение. Раскрасим клетки доски в «шахматном» порядке. Тогда, каждый жук должен переползти в клетку другого цвета, но белых и черных клеток на доске – разное количество, следовательно, хотя бы одна клетка доски должна остаться пустой.

Ответ. Верно.

7. Из трех квадратов, длины сторон которых (выраженные в сантиметрах) являются целыми числами, сложили прямоугольник.

а) Найдите его периметр, если его площадь равна 96 см²;
б) Найдите его площадь, если его периметр равен 50 см.

Решение.
Если рассмотреть все способы разбиения прямоугольника на три квадрата, то ясно, что существуют только два способа расположения данных квадратов (см. рис. 1, 2), первый из которых (в каждом из пунктов) противоречит условию. Действительно, если площадь прямоугольника (см. рис. 1) равна 96 см², то площадь каждого квадрата – 32 см², что невозможно, так как 32 не является квадратом натурального числа. Если же периметр этого прямоугольника равен 50 см, то должно выполняться равенство: (а + 3а)•2 = 50, что невозможно ни при каких натуральных а, где а – длина стороны маленького квадрата. Для прямоугольника на рис. 2 получим: а) площадь маленького квадрата равна 16 см², значит, его сторона – 4 см, то есть измерения прямоугольника – 12 см и 8 см; б) Так как сторона маленького квадрата в два раза меньше, чем большого, составляем уравнение: 2а + 3а = 25; a = 5; измерения прямоугольника – 10 см и 15 см.

Ответ. а) 40 см; б) 150 см².

8. На острове живут только лжецы и рыцари. Лжецы всегда лгут, рыцари всегда говорят правду. Встретились три островитянина: Ах, Ох и Ух. Ах сказал: «Мы все – лжецы». Ох ответил: «Ровно один из нас – рыцарь». Ух промолчал. Определите, кто есть кто.

Решение: Из высказывания Аха следует, что Ах не может быть рыцарем, значит, Ах – лжец. Следовательно, среди троих есть хотя бы один рыцарь. Если Ох солгал, то он лжец, но тогда рыцарь действительно один: Ух. Значит, Ох не может лгать, то есть, Ох – рыцарь, и тогда рыцарь действительно один. Следовательно, Ух – лжец.