Математическая олимпиада «Царицыно»
В прошедшем учебном году в целях развития интеллектуального потенциала учащихся и обмена опытом работы с одаренными детьми по инициативе кафедры математики и при поддержке директора ГОУ ЦО «Царицыно» № 548 ЮАО г.Москвы Е.Л.Рачевского на базе центра прошел Международный интеллектуальный турнир «Царицыно». Приглашение на участие в турнире было принято руководителями ряда образовательных учреждений городов Калининграда, Нижнего Новгорода, Киева, Минска. В рамках данного турнира для учащихся были проведены интеллектуальные соревнования по физике, математике и экономике, прочитаны познавательные лекции, поведены круглые столы с руководителями команд и учителями центра, во время которых были обсуждены проблемы и перспективы профильного образования, состоялся обмен опытом.
Одним из центральных мероприятий турнира стала олимпиада по математике, организованная для параллелей 6–11-х классов, задания которой были составлены автором данной статьи. Многие из предложенных задач не обладают абсолютной новизной, одни из них встречаются в известных сборниках с олимпиадными задачами, другие являются компиляцией, в третьих изменен текст или вопрос. Идеи решения всех задач хорошо известны. При составлении заданий предполагалось, что первые задачи может решить любой школьник, пожелавший принять участие в олимпиаде, а последние задания — по силе учащимся, увлеченным математикой. Автор надеется, что предлагаемый материал поможет учителям при подготовке к проведению школьных олимпиад и турниров, спецкурсов и факультативных занятий.
6 класс
1. В автобусе имеются одноместные и двухместные сидения. Кондуктор заметил, что когда в автобусе сидело 13 человек, то 9 сидений были полностью свободными, а когда сидело 10 человек, то полностью свободными были 6 сидений. Сколько сидений было в автобусе?
2. Прямоугольник составлен из шести квадратов (рис.1). Найдите сторону самого большого квадрата, если сторона самого маленького равна 1.

Рис. 1
3. В классе 26 учеников. Они сидят за 13 партами так, что ровно половина всех девочек в классе сидят с мальчиками. Можно ли пересадить учеников класса за те же 13 парт так, чтобы ровно половина всех мальчиков класса сидели с девочками?
4. На острове живут 100 человек, причем некоторые из них всегда лгут, а остальные говорят только правду. У каждого жителя острова есть только один любимый вид спорта из набора: теннис, футбол, гимнастика, шахматы и фигурное катание. Каждому островитянину был задано пять вопросов:
1) Любите ли вы футбол?
2) Любите ли вы теннис?
3) Любите ли вы гимнастику?
4) Любите ли вы шахматы?
5) Любите ли вы фигурное катание?
На первый вопрос утвердительно ответили 27 человек, на второй — 30; на третий — 42; на четвертый — 34, а на пятый — 21. Сколько лжецов живет на острове?
5 .Каждое из чисел x1, x2, x3, ..., xn равно либо 1, либо –1, причем
x1![]() x2
+ x2
x2
+ x2![]() x3
+ x3
x3
+ x3![]() x4
+ ... + xn
x4
+ ... + xn![]() x1
= 0.
x1
= 0.
Может ли n быть равным 2006?
7 класс
1. Разрежьте фигуру (по границам клеток) на 3 равные (одинаковые по форме и величине) части (рис. 2).

Рис. 2
2. Два пешехода вышли на рассвете. Каждый шел с постоянной скоростью. Один шел из А в В, а другой — из В в А. Они встретились в 12 часов дня и, не прекращая движения, пришли: один в В в 16 часов, а другой в А в 21 час. В котором часу в тот день был рассвет?
3. Имеется 10 карточек, каждая из которых выкрашена с одной стороны в красный, а с другой — в синий цвет. Карточки разложили в виде полосы так, что у семи карточек сверху оказался синий цвет. За один ход разрешается переворачивать любые две карточки. Можно ли добиться того, чтобы все карточки имели сверху красный цвет? В случае положительного ответа укажите способ достижения цели.
4. На доске были записаны первые 20 натуральных чисел. Одно из них стерли, и оказалось, что среди оставшихся 19 чисел есть число, равное среднему арифметическому этих 19 чисел. Какое число стерли?
5. Можно ли записать в строку 20 чисел так, чтобы сумма любых трех последовательных чисел была положительна, а сумма всех 20 чисел была отрицательна?
8 класс
1. В классе присутствуют учитель и несколько учеников. Найдите число учеников, если известно, что возраст учителя на 24 года больше среднего возраста учеников и на 20 лет больше среднего возраста всех присутствующих в классе.
2. Пусть a1, a2, ..., an — такие числа, что a1 + a2 + ... + an = 0. Сравните значение выражения
S = a1![]() a2
+ a1
a2
+ a1![]() a3
+ ... + an–1
a3
+ ... + an–1![]() an
и 0,
an
и 0,
если в сумму входят все возможные произведения ai![]() aj,
i ≠ j.
aj,
i ≠ j.
3. Биссектриса равнобедренного треугольника, проведенная из вершины, вдвое меньше другой биссектрисы. Найдите углы треугольника.
4. Некоторое натуральное число N делят с остатком на все натуральные числа, меньшие N. Сумма всех различных остатков оказалась равной N. Найдите N.
5. В клетках таблицы размером 10x20 расставлены 200 различных чисел. В каждой строке отмечены два наибольших числа красным цветом, а в каждом столбце отмечены два наибольших числа синим цветом. Какое наименьшее число чисел в таблице закрашено как красным, так и синим цветом?
9 класс
1. Сравните:где n! = 1![]() 2
2![]() 3
3![]() ...
...![]() n.
n.
2. Решите в натуральных числах уравнение
y + x2006 = НОК(х; у),
где НОК(х; у) — наименьшее общее кратное чисел х и у.
3. Существуют ли две трапеции, основания первой из которых соответственно равны боковым сторонам второй, а основания второй — боковым сторонам первой?
4. Решите неравенство
[2x]![]() {2x}
< 2x – 1,
{2x}
< 2x – 1,
где [a] — целая часть числа a, то есть наибольшее целое число, не превосходящее a; {a} — дробная часть числа a, то есть {a} = a – [a].
5. Можно ли записать в строку 50 чисел так, чтобы сумма любых 17 последовательных чисел была положительна, а сумма любых 10 последовательных чисел была отрицательна?
10 класс
1. Последовательность {an} задается следующим образом: a1 = 1,2. Пусть [a] — целая часть числа a, то есть наибольшее целое число, не превосходящее a; {a} — дробная часть числа a, то есть {a} = a – [a]. Решите уравнение
![]()
3. Найдите все функции f, удовлетворяющие при любых действительных x и y уравнению
f(x – y) = f(x) + f(y) – 2xy.
4. Точка пересечения высот равнобедренного треугольника лежит на вписанной в него окружности. Найдите отношение сторон треугольника.
5. Кучка из 25 камней произвольным образом делится на две кучки, любая из имеющихся кучек снова делится на две и т.д., пока каждая кучка не будет состоять из одного камня. При каждом делении какой-либо кучки на две записывается произведение чисел камней в получающихся двух кучках. Пусть S — сумма всех записанных чисел. Какие значения может принимать S?
11 класс
1. Найдите наименьшее значение выражения
![]()
2. Найдите значение выражения
1!![]() 3
– 2!
3
– 2!![]() 4
+ 3!
4
+ 3!![]() 5
– 4!
5
– 4!![]() 6
+ ... – 2006!
6
+ ... – 2006!![]() 2008
+ 2007!,
2008
+ 2007!,
где n! = 1![]() 2
2![]() 3
3![]() ...
...![]() n.
n.
3. В равнобедренную трапецию ABCD
(AB = CD) вписана окружность. Пусть M — точка касания
окружности со стороной CD, K — точка пересечения окружности с
отрезком AM, L — точка пересечения окружности с отрезком BM.
Вычислите величину ![]()
4. Сечение куба плоскостью — пятиугольник. Докажите, что площадь этого пятиугольника меньше произведения двух самых длинных его сторон.
5. Найдите наименьшую возможную сумму 10 различных натуральных чисел таких, что произведение любых пяти из них — четно, а сумма всех 10 чисел — нечетна.
Ответы, указания, решения
6 класс
1. 16 сидений.Если в автобусе находятся 13 человек, то наименьшее число занятых сидений равно 7, а наибольшее 13, значит, в автобусе всего сидений не менее 7 + 9 = 16 и не более 13 + 9 = 22. Если же в автобусе находятся 10 человек, то наименьшее число занятых сидений равно 5, а наибольшее 10, значит, в автобусе всего сидений не менее 5 + 6 = 11, но не более 10 + 6 = 16. Значит, в автобусе 16 сидений.
2. Сторона наибольшего квадрата равна 7.
Пусть сторона квадрата 2 равна х (рис. 3),
тогда сторона квадрата 3 равна х + 1, квадрата

Рис. 3
3. Пересадка невозможна.
Половина всех девочек сидят с мальчиками, то есть число девочек четно. Поскольку другая половина девочек сидят с девочками, то число, равное половине девочек, также четно. Значит, число девочек кратно четырем. Если бы пересадка была возможна, то и число мальчиков было бы кратно четырем, а значит, и количество всех учеников должно было бы делиться на четыре. Число 26 на 4 не делится, значит, пересадить невозможно.
4. На острове 18 лжецов.
Если бы все жители острова говорили правду, то было бы дано 100 утвердительных ответов. Каждый лжец своими ответами увеличивает число утвердительных ответов на 3. Всего было дано 27 + 30 + 42 + 34 + 21 = 154 утвердительных ответа, поэтому количество лжецов равно
![]()
5. n равным 2006 быть не может.
Рассмотрим числа
у1 = х1х2, у2 = х2х3 , ..., уn = хnх1.
Каждое из них равно либо 1, либо –1. Так как их сумма равна
0, то количество единиц равно количеству единиц со знаком «–», то есть n —
четное или n = 2k , где k — число отрицательных чисел уi
и число положительных чисел уi. Произведение
у1![]() у2
у2![]() ...
...![]() уn
= (x1
уn
= (x1![]() x2
x2![]() ...
...![]() xn)2
> 0, поэтому число отрицательных сомножителей k четно.
Следовательно, n делится на 4. Число 2006 не делится на 4, значит, n
равным 2006 быть не может.
xn)2
> 0, поэтому число отрицательных сомножителей k четно.
Следовательно, n делится на 4. Число 2006 не делится на 4, значит, n
равным 2006 быть не может.
7 класс
1. Смотри рис. 4.

Рис. 4
2. Рассвет наступил в 6 часов утра.
Пусть место встречи — пункт Р, скорость движения
первого пешехода — х км/ч, а второго — у км/ч. Тогда РВ = 4х
км, а РА= 9у км. Первый пешеход прошел расстояние РА за ![]() ч,
а второй расстояние РВ за
ч,
а второй расстояние РВ за ![]() ч. Так как
ч. Так как ![]() и время движения первого
пешехода до встречи равно
и время движения первого
пешехода до встречи равно ![]() ч. Значит, рассвет наступил в 12 – 6 = 6 ч утра.
ч. Значит, рассвет наступил в 12 – 6 = 6 ч утра.
3. Нельзя.
Поставим в соответствие каждой красной стороне карточки какое-либо четное число, каждой синей — нечетное, а полосе из карточек — сумму соответствующих чисел. Начальной сумме соответствует нечетное число. Переворот любых двух карточек не меняет четности первоначальной суммы, а значит, получить в итоге четное число, соответствующее красной полосе, нельзя.
4. 1 или 20.
С одной стороны, сумма оставшихся 19 чисел кратна 19, так как
она равна произведению одного из оставшихся чисел и 19; с другой стороны,
минимальное значение оставшейся суммы равно 1 + 2 + ... + 19 = 190, а
максимальное значение равно 2 + 3 + ... + 20 = 209.
Из чисел 190, ..., 209
кратными 19 являются только 190 и 209. Значит, с доски могли стереть либо
(1 + 2 + ... + 20) – 190 = 20, либо
(1 + 2 + ... + 20) – 209 = 1.
5. Можно.
Например:
–a, b, b, –a, b, b, ..., –a, b, b, –a, b,
где a и b таковы, что 2b – a > 0 и 13b – 7a < 0. Одно из решений: a = 25, b = 13.
8 класс
1. 5 учеников.2. S ≤ 0, так как

3. 36°, 36°, 108°.
Пусть A — вершина равнобедренного треугольника ABC,
а его биссектриса AM вдвое меньше биссектрисы BD (рис. 5). На
продолжении биссектрисы AM за точку M отложим отрезок MK,
равный AM. Тогда BK ![]() AD и AK = 2AM = BD. Если P — точка
пересечения биссектрис треугольника ABC, то BP = KP.
Обозначим
AD и AK = 2AM = BD. Если P — точка
пересечения биссектрис треугольника ABC, то BP = KP.
Обозначим ![]() ABP
через α.
ABP
через α.
Тогда ![]() PKB
=
PKB
= ![]() PBK
= 3α.
Поскольку BK = AB, то
PBK
= 3α.
Поскольку BK = AB, то ![]() BAK
=
BAK
=![]() AKB
=
AKB
= ![]() PKB
= 3α.
PKB
= 3α.
Из прямоугольного треугольника AMB находим, что
![]() BAK =
BAK =
![]() BAM
= 90°
–
BAM
= 90°
– ![]() ABM
= 90°
– 2α.
ABM
= 90°
– 2α.
Из уравнения 3a
= 90°
– 2a
находим, что α = 18°.
Следовательно, ![]() ABC
= 36°.
ABC
= 36°.

Рис. 5
4. N = 10.
5. 3 числа.
9 класс
1. ![]()
Рассмотрим цепочку равенств:

2. В натуральных числах решений нет.
Преобразуем уравнение к виду y = НОК(х; у)
– x2006. Поскольку НОК(х; у) делится на х,
то и НОК(х; у) – x2006 также делится на х,
значит, и у делится на х. Поэтому НОК(х; у) = у,
тогда х2006 = 0,
то есть х = 0, а 0 ![]() N.
N.
3. Нет.
Через вершину B меньшего основания BC трапеции ABCD проведем прямую, параллельную боковой стороне CD, до пересечения с основанием AD в точке K (рис. 6).

Рис. 6
Тогда
AK = AD – DK = AD – BC, BK = CD
(поскольку BCDK — параллелограмм),
AD – BC = AK > |AB – BK| = |AB – CD|,
то есть в любой трапеции разность оснований больше разности боковых сторон. Значит, таких трапеций не существует.
4. x ![]() [1; +∞).
[1; +∞).
Преобразуем неравенство к виду
[2x]![]() {2x}
< {2x} + [2x] – 1; ([2x] – 1)
{2x}
< {2x} + [2x] – 1; ([2x] – 1)![]() ({2x}
– 1) < 0.
({2x}
– 1) < 0.
Так как значение дробной части числа меньше 1, то неравенство равносильно
[2x] > 1; [2x] ≥ 2; 2x ≥ 2; x ≥1.
5. Нельзя.
Пусть a1, a2, ..., a50 — искомые числа. Тогда
a1 + a2 + ... + a34 > 0, а a1 + a2 + ... + a30 < 0.
Следовательно,
a31 + a32 + a33 + a34 > 0.
Аналогично докажем, что
a35 + a36 + a37 + a38 > 0, a39 + a40 + a41 + a42 > 0
и т.д. Складывая эти неравенства, получим, что
a31 + a32 + ... + a50 > 0,
что противоречит условию задачи.
10 класс
1. Оценим ![]()
 .
.
2. 1,5.
Пусть [20,06x – 20,07] = n, тогда верно, что
![]()

Поскольку n — целое число, то n = 10, и значит, х = 1,5.
3. f(x) = x2.
Пусть x = y, тогда
f(0) = f(x) + f(x) – 2x2;
f(x) = x2 + 0,5![]() f(0).
f(0).
Пусть x = y = 0, тогда f(0) = 0.
4. 3 : 3 : 4.
5. 300.
Пусть кучка из 25 камней была разбита на две кучки по x и y камней. Тогда, заметив, что
![]()
получим после первого разделения число
![]()
Если кучку из x камней разбить на кучки из x1 и x2 камней, а кучку из y камней разбить на кучки из y1 и y2 камней, то

Проводя аналогичные действия, получим, что

11 класс
1.
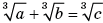
Следовательно, наименьшее значение выражения равно ![]()
2. 1.
1!![]() 3
– 2!
3
– 2!![]() 4
+ 3!
4
+ 3!![]() 5
– 4!
5
– 4!![]() 6
+ ... – 2006!
6
+ ... – 2006!![]() 2008
+ 2007! =
2008
+ 2007! =
= 1!![]() (2
+ 1) – 2!
(2
+ 1) – 2!![]() (3
+ 1) + 3!
(3
+ 1) + 3!![]() (4
+ 1) – 4!
(4
+ 1) – 4!![]() (5
+ 1) +
(5
+ 1) +
+ ... – 2006!![]() (2007
+ 1) + 2007! =
(2007
+ 1) + 2007! =
= 2! + 1! – 3! – 2! + 4! + 3! – 5! – 4! + ... – 2007! – 2006! = 1.
3. 10.
Пусть N — середина стороны AD, a = AN,
x = AK, y = AM,
a =
![]() ADM.
ND = DM = a, и по теореме косинусов
ADM.
ND = DM = a, и по теореме косинусов
y2 = 4a2 + a2 – 4a2cos α= a2(5 – 4cos α).
С другой стороны, по теореме о секущей и касательной имеем:
xy = a2.
Поэтому ![]()
Аналогично,
![]()
Следовательно,
![]()
4. Куб имеет 3 пары параллельных граней, поэтому если сечение — пятиугольник, то он имеет 2 пары параллельных сторон и может быть получен из некоторого параллелограмма отрезанием треугольника прямой, пересекающей две его соседние стороны. Площадь сечения меньше площади параллелограмма, а площадь параллелограмма не превосходит произведения двух своих смежных сторон. Произведение длин двух сторон пятиугольника не больше длин двух его самых длинных сторон.
5. 65.
Так как произведение любых пяти чисел из набора четно, то
нечетных чисел меньше 5.
Так как сумма всех чисел нечетна, то в наборе нечетное
число нечетных чисел. Значит, в наборе либо 3, либо 1 нечетное число. Сумма
чисел набора будет наименьшей, если мы возьмем первые подряд идущие четные и
нечетные числа. Причем нечетных чисел нужно брать 3, а не 1, так как
2 + 4 + ... + 14 + 1 + 3 + 5 < 2 + 4 + ... + 18 + 1.
Таким образом, наименьшей будет сумма
2 + 4 + 6 + 8 + 10 + 12 + 14 + 1 + 3 + 5 = 65.