Рассмотрим сначала следующую задачу.
Дан непрямоугольный треугольник ABC с высотами AA1, BB1 и CC1. Докажите, что прямые Эйлера (см. ниже) треугольников AB1C1, A1BC1, A1B1C пересекаются в такой точке P окружности девяти точек треугольника ABC, для которой один из отрезков PA1, PB1, PC1 равен сумме двух других отрезков.
Автором этой задачи является известный французский геометр Виктор Тебо, а ее решение приведено в [1]. В нашей статье будет рассказано про некоторые обобщения данной задачи.
Упражнения
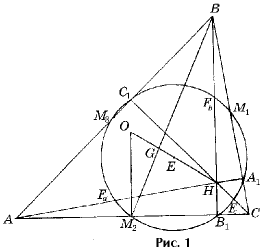
1. Докажите, что для произвольного неравностороннего треугольника ABC его ортоцентр (точка пересечения высот) H, точка пересечения медиан G и центр O описанной окружности лежат на одной прямой, называемой прямой Эйлера этого треугольника, причем OG : GH = 1 : 2 (рис. 1).
2. Докажите, что середины сторон треугольника ABC, основания его высот и середины отрезков, соединяющих ортоцентр с вершинами треугольника, лежат на одной окружности, которая называется окружностью девяти точек треугольника ABC. Центр этой окружности совпадает с серединой отрезка OH, а ее радиус равен половине радиуса описанной окружности треугольника ABC (рис. 1).
3. Докажите, что радиус описанной окружности и высота треугольника, проходящие через одну из его вершин, образуют равные углы со сторонами треугольника, пересекающимися в той же вершине.
4. Пусть AA1, BB1, CC1 – высоты непрямоугольного треугольника ABC, Р BAC = a, Р CBA = b, Р ACB = g. Докажите, что:
а) треугольники AB1C1, A1BC1, A1B1C подобны треугольнику ABC с коэффициентами подобия | cos a |, | cos b |, | cos g | соответственно;
б) прямые Эйлера треугольников AB1C1, A1BC1, A1B1C пересекаются в точке P, лежащей на окружности девяти точек треугольника ABC.
5. Докажите, что прямая Эйлера остроугольного треугольника пересекает его наибольшую и наименьшую стороны, а прямая Эйлера тупоугольного треугольника – его наибольшую и среднюю стороны.
Заметим, что решение упражнения 2 можно найти в [2], а упражнения 4 б) – в [1].
Лемма 1. Прямая Эйлера треугольника ABC пересекает его стороны AB и BC в точках M и N соответственно. Тогда прямая Эйлера треугольника MBN параллельна стороне AC.
Доказательство. Предположим, что D ABC остроугольный (рис. 2), тогда из упражнения 5 следует, что AB и BC – наибольшая и наименьшая стороны D ABC (будем считать для определенности, что AB > BC). Пусть H и H1 – ортоцентры, O и O1 – центры, а R и R1 – радиусы описанных окружностей треугольников ABC и MBN; D – основание высоты BD треугольника MBN, Р ABC = b, Р DBH = b1, Р DBO = b2.
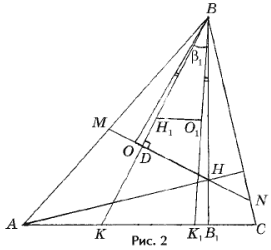
Поскольку Р MBO = Р NBH и Р MBD = Р NBO1 (упражнение 3), то Р HBO1 = Р DBO = b2. Из упражнения 4а) следует, что BH = 2Rcos b, поэтому из прямоугольных треугольников OBD и HBD
BD = BO cos b2 = Rcos b2 = BH cos b1 = 2R cos bcos b1, откуда cos b2 = 2cos b cos b1.
С другой стороны, из прямоугольных треугольников KBB1 и K1BB1
и
Таким образом, D BH1O1 " D BKK1 и H1O1 || KK1. На рис. 2 точка D принадлежит отрезку OH. Случай, когда точка D лежит вне отрезка OH, разберите самостоятельно.
Упражнения
6. Проведите доказательство леммы 1 для тупоугольного треугольника.
7. Прямая Эйлера треугольника параллельна одной из его сторон.
Докажите, что:
а) произведение тангенсов углов, прилежащих к этой стороне, равно 3;
б) данный треугольник остроугольный.
8. Докажите, что прямая Эйлера разностороннего
а) остроугольного треугольника ABC отсекает от него остроугольный треугольник T, причем средние по величине углы треугольников ABC и T совпадают;
б) Тупоугольного треугольника ABC отсекает от него разносторонний тупоугольный треугольник T, причем минимальные углы треугольников ABC и T совпадают.
9. Докажите, что если один из углов остроугольного треугольника равен 60°, то прямая Эйлера этого треугольника отсекает от него правильный треугольник.
10. Докажите, что если ни один из углов разностороннего остроугольного треугольника не равен 60°, то прямая Эйлера этого треугольника отсекает от него разносторонний остроугольный треугольник.
Определение. Пусть прямая Эйлера треугольника ABC не проходит ни через одну из его вершин и отсекает от него треугольник T1, прямая Эйлера треугольника T1 отсекает от него треугольник T2, …, прямая Эйлера треугольника Tn–1 – треугольник Tn (n = 1, 2, 3, …, T0 = D ABC). Назовем прямой Эйлера порядка n или n–прямой Эйлера треугольника ABC прямую Эйлера треугольника Tn–1.
Ясно, что 1–прямая Эйлера треугольника совпадает с прямой Эйлера этого треугольника. Поскольку прямая Эйлера равнобедренного или прямоугольного треугольника проходит через одну из его вершин, то для этих треугольников n-прямые Эйлера не определены при n > 1. Из упражнений 8–10 следует, что для всех остальных треугольников n–прямые Эйлера определены для любых натуральных n, за исключением таких остроугольных треугольников ровно один из углов которых равен 60°. В самом деле, для остроугольного треугольника с одним из углов в 60° n–прямая Эйлера не определена при n l 2 (упражнение 9).
Из определения n–прямых Эйлера и леммы 1 вытекает, что все n–прямые Эйлера нечетного порядка параллельны друг другу и прямой Эйлера треугольника ABC, а все n–прямые Эйлера четного порядка параллельны друг другу и одной из сторон треугольника ABC (средней для остроугольного треугольника и наименьшей для тупоугольного, рис. 3).
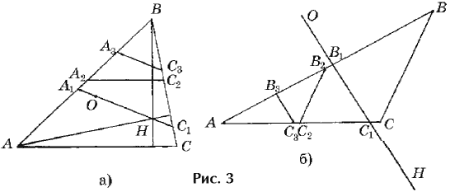
В дополнение к обозначениям упражнения 4 будем считать, что в D ABC a < b < g, H – ортоцентр, Fa, Fb, Fc – середины отрезков AH, BH, CH.
Теорема 1. Дан разносторонний остроугольный треугольник ABC, ни один из углов которого не равен 60°. Тогда точки пересечения прямых Эйлера порядка n треугольников AB1C1, A1BC1, A1B1C являются при n > 1 вершинами треугольников Tn, подобных треугольнику ABC, причем при четных n треугольники Tn гомотетичны друг другу и треугольнику A1BC1 с центром гомотетии в точке Fb, а при нечетных n – гомотетичны друг другу с центром гомотетии в точке P.
Доказательство. Поскольку ни один из углов разностороннего остроугольного D ABC не равен 60°, то его n–прямые Эйлера определены для всех натуральных n.
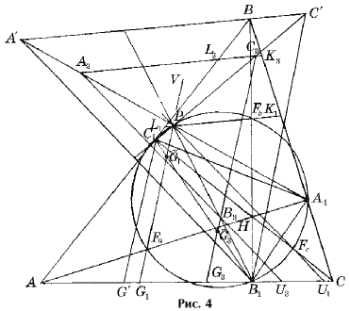
Рассмотрим сначала n = 3. Напомним, что в силу принятых обозначений Р CBA = b – средний по величине угол D ABC (рис. 4). Треугольники AB1C1, A1BC1, A1B1C подобны D ABC (упражнение 4 а) и, значит, n–прямые Эйлера этих треугольников также определены для любых натуральных n, причем Р C1BA1 = Р AB1C1 = Р CB1A1 = b – средние по величине углы в треугольниках AB1C1, A1BC1,
A1B1C.
Поскольку прямые Эйлера этих треугольников
пересекаются в точке P, лежащей на окружности
девяти точек D ABC (упражнение 4 б), то Р FaPFc = Р FaFbFc,
как вписанные, опирающиеся на одну и ту же дугу
окружности девяти точек. Но Р FaFbFc
= Р
ABC = b, так как D FaFbFc
гомотетичен D ABC с центром гомотетии в точке H и
коэффициентом 
. Аналогично
Р FbPFc = a, Р FaPFb = 180° – g,
Р VPFb = 180° – Р FaPFb = g,
т. е. острые углы между прямыми Эйлера треугольников AB1C1, A1BC1, A1B1C равны углам треугольника ABC, а поскольку по лемме 1 3–прямые Эйлера этих треугольников параллельны их прямым Эйлера, то и углы треугольника T3 = A3B3C3 равны углам D ABC, откуда следует их подобие.
Покажем теперь, что вершины треугольника T3 лежат на прямых, соединяющих точку P с точками A1, B1, C1. Пусть G1, G3, U1, U3 – соответственно точки пересечения прямой Эйлера и 3–прямой Эйлера треугольников AB1C1 и CB1A1 со стороной AC (рис. 4), а B3R и B3RR – точки пересечения 3–прямых Эйлера этих треугольников с отрезком PB1. Тогда
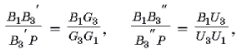
так как G3B3R || G1P
и U3B3RR || U1P. Но 
в
силу подобия треугольников AB1C1
и CB1A1, поэтому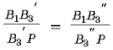 
и B3R є B3RR є B3, т. е. точка B3
пересечения 3–прямых Эйлера треугольников AB1C1
и CB1A1 лежит на отрезке PB1.
Аналогично показывается, что точки A3 и C3 лежат на прямых PA1 и PC1. Понятно, что доказательство этих фактов для произвольного треугольника T2l + 1 будет точно таким же.
Итак, треугольники T2l + 1, l = 1, 2, … подобны треугольнику ABC, а их вершины A2l + 1, B2l + 1, C2l + 1 лежат на прямых PA1, PB1, PC1. Отсюда вытекает, что треугольники T2l + 1, l = 1, 2, … гомотетичны с центром гомотетии P. Далее, Р C1PB3 = Р C1PB1 = Р C1A1B1 = 180° – 2a и Р B3PC3 = 180° – Р C1PB3 = 2a. Аналогично, Р A3PC3 = 2b, Р A3PB3 = 2g, т. е. стороны треугольника A3B3C3 видны из точки P под углами 2a, 2b, 2g и, таким образом, точка P совпадает с центром описанной окружности D A3B3C3, а следовательно, и треугольников T2l + 1, l = 2, 3, …
При l ® Ґ треугольники T2l + 1
стремятся к предельному треугольнику D1 = ARB1C R, одна из
вершин которого совпадает с B1.
Поскольку радиусы описанных окружностей
треугольников D1 и ABC равны PB1 и R,
то коэффициент подобия треугольника D1
треугольнику ABC равен 
Но точки
P и B1 лежат на окружности девяти
точек D ABC,
поэтому хорда PB1 не превосходит
диаметра этой окружности, равного R
(упражнение 2) и k Ј 1.
Выясним, когда k = 1. При k = 1 PB1 = R, т. е. хорда PB1 является диаметром и Р PFbB1 = 90° = Р PFbB. Так как Fb – центр описанной окружности D A1BC1, подобного D ABC, то это означает, что данному условию удовлетворяют треугольники ABC, прямая Эйлера которых перпендикулярна диаметру описанной окружности, проходящему через вершину среднего угла D ABC. Для таких треугольников ABC треугольник D1 симметричен D ABC относительно средней линии, параллельной стороне AC (рис. 5).
Итак, в любом случае коэффициенты подобия треугольников T2l + 1 и ABC меньше единицы, и ни один из треугольников T2l + 1 не может быть равен D ABC.
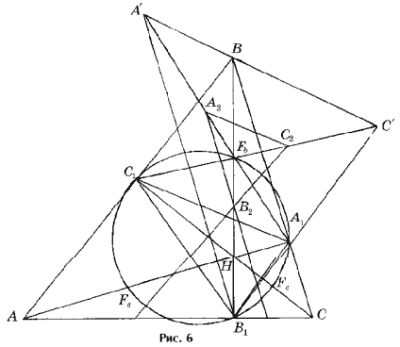
Доказательство для треугольников Tn с четными номерами аналогично приведенному выше. В этом случае коэффициент подобия предельного треугольника D2 треугольнику ABC равен cos (g – a) < 1 (a < g, рис. 6).
Заметим, что если прямая Эйлера D ABC параллельна стороне AC, то точка P совпадает с точкой Fb и все треугольники Tn имеют общий центр гомотетии Fb (рис. 7).
Утверждение теоремы 1 справедливо и для произвольных разносторонних тупоугольных треугольников ABC со следующим незначительным изменением в случае четных n: треугольники T2m гомотетичны друг другу и D AB1C1 с центром гомотетии в точке Fa. Укажем еще на некоторые отличия от остроугольного треугольника: для тупоугольного D ABC коэффициенты гомотетии треугольников T2m и D AB1C1 могут менять знак (с положительного на отрицательный), т. е. треугольники T2m как бы совершают «кульбит». Если рассмотреть три тупоугольных треугольника ABC, ACH, BCH, где H – ортоцентр D ABC, а треугольник ABH – разносторонний, то для двух из них центры гомотетии треугольников T2m совпадают, а коэффициенты гомотетии треугольников T2m не меняют знак лишь для одного из треугольников ABC, ACH, BCH (здесь одинаково обозначены через T2m элементы трех последовательностей T2m(1), T2m(2), T2m(3), треугольников ABC, ACH, BCH, m = 1, 2, …, напомним, что в D ABC тупым является угол ACB). Поскольку прямая Эйлера тупоугольного треугольника не параллельна ни одной из его сторон (упражнение 7), то для тупоугольного треугольника центры гомотетии треугольников T2m и T2l + 1 (m, l = 1, 2, …) не могут совпадать.
Попытайтесь самостоятельно разобраться в приведенных здесь фактах.
Лемма 2. Прямая, проходящая через точку G пересечения медиан треугольника ABC, пересекает его стороны AB и BC в точках M и N.
Тогда 
Доказательство. Пусть D, E,
S, L – основания перпендикуляров,
опущенных соответственно из точек A, K, B,
C на прямую MN (рис. 8, K – середина AC).
Тогда 
как средняя линия
прямоугольной трапеции ACLD. Из подобия
прямоугольных треугольников KEG и BSG
следует, что 
(напомним, что G –
точка пересечения медиан треугольника ABC).
Итак,
BS = 2KE = AD + CL.
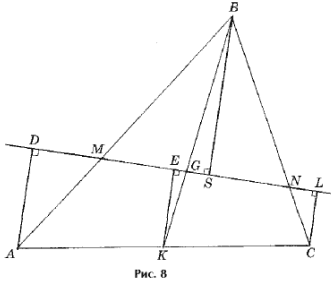
Из подобия прямоугольных треугольников ADM и BSM, CLN и BSN выводим, что
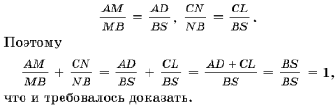
Упражнения
11. В разностороннем остроугольном треугольнике ABC Р ABC = 60°, прямая Эйлера этого треугольника пересекает его стороны AB и BC в точках M и N. Докажите, что AM + CN = MN.
12. Найдите геометрическое место центров тяжести всевозможных треугольников BAC, угол BAC которых общий, а сумма сторон AB и BC постоянна (AB + BC = d > 0).
13. Пусть n–прямые Эйлера
треугольника ABC пересекают его стороны AB
и BC в точках An и Cn (n = 1, 2, 3),
причем 
Докажите, что
тогда и только тогда, когда
прямая A1C1 параллельна стороне AC;
г) коэффициент подобия треугольников A2BC2 и ABC равен k;
д) коэффициент подобия треугольников A3BC3 и A1BC1 равен k.
14. Прямые Эйлера порядка n треугольника ABC определены для любых натуральных n и пересекают его стороны AB и BC в точках An и Cn, n = 1, 2, … Докажите, что площади S0, S1, …, Sn, … четырехугольников AA1C1C, A1A2C2C1, …, AnAn + 1Cn + 1Cn образуют геометрическую прогрессию.
Теорема 2. Пусть n–прямые Эйлера треугольника ABC определены для любых натуральных n. Тогда сумма расстояний от двух вершин треугольника T2l + 1 = A2l + 1B2l + 1C2l + 1 до двух одноименных вершин треугольника A1B1C1 равна сумме расстояния между третьими вершинами этих треугольников с утроенным радиусом описанной окружности треугольника T2l + 1.
Доказательство. Рассмотрим
остроугольный D ABC (рис. 4). Обозначим через
d1, d2, d3, длины
отрезков PA1, PB1, PC1, а
через R3 – радиус описанной окружности D A3B3C3.
Тогда, поскольку PFb || A3C3,
получаем по теореме Фалеса 
.
Аналогично 
Из подобия треугольников A1BC1
и B1AC1 следует, что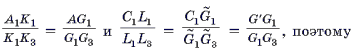 
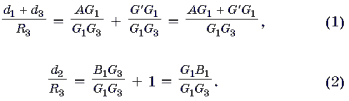
Так как прямая Эйлера треугольника проходит через точку пересечения его медиан (упражнение 1), то по лемме 2
откуда G RG1 + AG1 = G1B1. Подставив найденное выражение в (1) и учитывая (2), получим
Пусть теперь dA(2l+1), dB(2l+1), dC(2l+1) – расстояния от вершин A2l+1, B2l+1, C2l+1 до точек A1, B1, C1 соответственно, R2l+1 – радиус описанной окружности треугольника T2l+1. Тогда
dA(2l+1) = A2l+1P + PA1 = R2l+1 + d1,
dB(2l+1) = PB1 – PB2l+1 = d2 – R2l+1,
dC(2l+1) = C2l+1P + PC1 = R2l+1 + d3
и
dA(2l+1) + dC(2l+1) = 2R2l+1 + d1 + d3 =
= 2R2l+1 + d2 = dB(2l+1) + 3R2l+1 .
В случае l = 0, рассмотренном в задаче Тебо, треугольник T2l+1 вырождается в точку, при этом R1 = 0.
Упражнение 15. Докажите теорему 2 для тупоугольного треугольника.
Литература
1. Куланин Е. Об одном свойстве точек Фейербаха. «Математика», № 10/97.
2. Куланин Е. Связующая нить. «Математика», № 24/97.